Problem
Given a non-negative index k where k ≤ 33, return the $k^{th}$ index row of the Pascal’s triangle.
Note that the row index starts from 0.
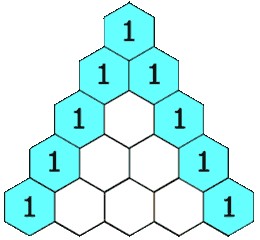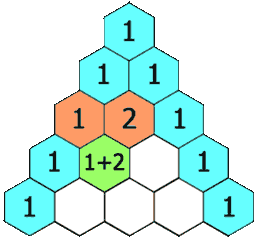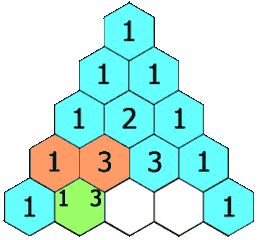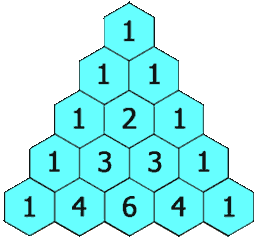
In Pascal’s triangle, each number is the sum of the two numbers directly above it.
Example:
1 | Input: 3 |
Follow up:
1 | Could you optimize your algorithm to use only O(k) extra space? |
Analysis
这是杨辉三角系列的第二题,分析也是建立在的基础上,请确保您已经了解第一题。这道题需要我们计算某一层的内容,而无需输出整一个杨辉三角。当然,基于第一题,我们可以把杨辉三角生成出来,然后挑选指定的行输出,但是这里我选用了一种更加节省空间的方法。
充分利用杨辉三角的特性,即每一行的元素依赖且仅依赖于上一行的元素,也就是说,我们可以交替用两个vector,就可以生成我们所需要的行了。生成每一行的方法与第一题一样,不同之处在于无需把新生成的行加入到result中,而是直接取代result,成为新的结果。
Solution
整体的代码与第一题很类似,这里只说不同的地方。使用一个变量temp和result交替使用,记得每次置空temp,每层结束后将temp赋值给result。
Code
1 | class Solution { |
运行时间:约0ms,超过100%的CPP代码。
Update On 08/13/2020
今天再次刷到了这道题,对比起第一次做,又有了新的想法,所以更新在这里。思路和上面是比较相似的,但这次从数学原理开始推导,也有优化了一下代码。
先看看杨辉三角的数学原理,每一行除了首尾外,第$i$个元素都等于上一行的第$i - 1$加上第$i$个元素。而杨辉三角实际上就是二项式系数,即第$n$层的第$k$个数字表示为$C_n^k$($n$和$k$从1开始)。所以根据上面这个性质,我们就能推导出组合数中的一个恒等式:
$$
C_n^k = C_{n-1}^{k - 1} + C_{n - 1}^{k}
$$
上面就是杨辉三角和组合数公式的数学联系。回到这道题目,我们只需要知道从上一行计算出下一行就可以了。因为是自上而下的计算,我们完全可以只使用一个数组。然后计算的时候不更新头尾两个位置的元素就可以了。代码如下:
1 | class Solution { |
Summary
这道题是杨辉三角的拓展题,技巧在于使用有限的线性空间来进行求解。只要第一题的算法写好了,稍加修改就可以实现了。这道题的分析到这里,谢谢!

