Halo

A magic place for coding

0%

求解矩阵的四种迭代法

Posted on Edited on Valine:

Introduction

  在之前我实现了求解低阶矩阵的一些算法。考虑线性方程组Ax=b，其中A为非奇异矩阵，当A是低阶稠密矩阵时，可以使用之前提到的中的高斯消元法以及列主
元消元法（详情请参考高斯消元法之讲解与代码实现）来进行求解。但是实际生活中工程技术产生的矩阵都是大型的稀疏矩阵（阶数很大，但零元素很多），当A是高阶稀疏矩阵时，就可以利用迭代法来进行求解。迭代法利用了A中零元素较多的特点，这对于计算机的存储和运算是很有利的。
  迭代法的基本思想是：对于线性方程组的第$k$行，假设除去$x_k$外，其他$x$已知，那么我就可以求出这一个$x_k$，考虑到矩阵稀疏的特点，每一行的计算就显得很容易了。通过迭代，每一行都基于之前算出的结果，对当前行的$x_k$进行更新，如果迭代向量具有收敛的性质，那么我们最后就可以逼近一个精确解。
  我们通过变换，可以将Ax=b等价变换为$x^* = Bx + f$。构造向量序列$$
x^{(k+1)} = Bx^{(k)} + f
$$，其中$k$表示迭代次数。
  如果$\displaystyle \lim_{x\to\infty}x^{(k)}$存在，则说明迭代法收敛，否则，该迭代法发散。所以我们每次使用迭代法求解矩阵的时候就需要判断矩阵是否收敛。
。
注意：在使用迭代法求解的时候，要确保是可以收敛到一个精确解的。这里给出一个判断矩阵收敛的定理：对于一个线性方程组，迭代法收敛的充要条件是矩阵B的谱半径ρ(B) < 1

  这里主要分析四种迭代方法：雅可比迭代法、高斯赛德尔迭代法、超松弛迭代法、共轭梯度法。

雅可比迭代法（Jocobi Method）

分析

  现在我来讲解雅可比迭代法。雅可比迭代法是对上述迭代过程的详细展开。对于线性方程组的系数矩阵A，可分解为三部分：
$$
A = \begin{bmatrix}
a_{11} & \
& a_{22} \
& & \ddots \
& & & a_{nn}
\end{bmatrix} -
\begin{bmatrix}
0\
-a_{21} & 0\
\vdots & \vdots & \ddots \
-a_{n-1,1} & -a_{n-1,2} & \cdots & 0 \
-a_{n1} & -a_{n2} & \cdots & -a_{n,n-1} & 0 \
\end{bmatrix} -
\begin{bmatrix}
0 & -a_{12} & \cdots & -a_{1,n-1} & -a_{1n} \
& 0 & \cdots & -a_{2,n-1} & -a_{2n} \
& & \ddots & \vdots & \vdots \
& & & 0 & -a_{n-1,n} \
& & & & 0 \
\end{bmatrix} = D-L-U
$$
设$a_{ii} \neq 0(i=1,2,…,n)$，可以得到Ax=b的雅可比迭代法：
$$
\begin{cases}
x^{(0)}, 初始向量\
x^{(k+1)} = Bx^{(k)} + f, k= 0,1,…,\
\end{cases}
$$
其中$B=I-D^{-1}A=D^{-1}(L+U)=J, f=D^{-1}b$，称J为解Ax=b的雅可比迭代法的迭代矩阵。
解Ax=b的雅可比迭代法的计算公式为：
$$
\begin{cases}
x^{(0)} = (x_1^{(0)},x_2^{(0)},…,x_n^{(0)})^T \
x_i^{(k+1)} = (b_i - \sum_{j=1,j \neq i}^na_{ij}x_j^{(k)}） / a_{ii},\
i = 1,2,…,n; k=0,1,…表示迭代次数。\
\end{cases}
$$
根据上述计算公式就可以使用雅可比迭代法求解了。

代码实现

Matlab代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
% 雅可比迭代法
function[xn]=jacobi(A,b,max)
n=size(A,1);
eps = 0.000001;
% 默认最大迭代次数
if nargin == 2
    max = 200;
end

% 初始化向量
x0=zeros(n,1);
xn=zeros(n,1);
x0(1)=1;

times = 0; % 记录迭代次数
while norm(xn-x0)>=eps && times <= max
    times=times+1;
    x0=xn;

    for i=1:n
        sum = 0;
        for j =1:n
            if (j~=i)
                sum = sum + A(i,j) * x0(j);
            end
        end
    xn(i)=(b(i)-sum)/A(i,i);
    end

    if(times>=max)
        return;
    end
end
% 输出迭代次数和结果
disp(times);
disp(xn);

高斯赛德尔迭代法（Gauss-Seidel Method）

分析

  高斯-赛德尔迭代法可以看作是对雅可比迭代法的优化改进。它的思路在于，更新每一步$x_k$的时候，可以利用已经更新$x_j(j < k)$的值，这样可以减少迭代次数，因为它计算每一个分量的时候是基于当前的最新分量。
设$a_{ii} \neq 0(i=1,2,…,n)$，可以得到Ax=b的高斯-赛德尔迭代法：
$$
\begin{cases}
x^{(0)}, 初始向量\
x^{(k+1)} = Bx^{(k)} + f, k= 0,1,…,\
\end{cases}
$$
其中$B=I-(D-L)^{-1}A=(D-L)^{-1}U=G,f=(D-L)^{-1}b.称G=(D-L)^{-1}U为解Ax=b的高斯赛德尔迭代法的迭代矩阵$。
求解Ax=b的高斯赛德尔迭代法计算公式为
$$
\begin{cases}
x^{(0)} = (x_1^{(0)},x_2^{(0)},…,x_n^{(0)})^T，初始向量 \
x_i^{(k+1)} = (b_i - \sum_{j=1,j \neq i}^{i-1}a_{ij}x_j^{(k+1)} - \sum_{j=i+1}^na_{ij}x_j^{(k)}） / a_{ii},\
i = 1,2,…,n; k=0,1,…表示迭代次数。\
\end{cases}
$$
这就是高斯赛德尔迭代法的计算公式。

代码实现

Matlab代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
% 高斯赛德尔迭代法
function[xn]=Gauss_Seidel(A,b, max)
n=size(A,1);

% 默认最大迭代次数
if nargin == 2
    max = 200;
end

eps = 0.000001; % 精度控制

% 初始化向量
x0=zeros(n,1);
xn=zeros(n,1);
x0(1)=1;

% 保证有解
if det(A) == 0
    return;
end

times = 0; % 迭代次数
while norm(xn-x0)>=eps && times <= max
    times=times+1;
    x0=xn;

    for i=1:n
        sum1 = 0;
        sum2 = 0;
        % 使用新的x
        for j =1:i-1
                sum1 = sum1 + A(i,j) * xn(j);
        end
        for j=i+1:n
            sum2 = sum2 + A(i,j) * x0(j);
        end
    xn(i)=(b(i) - sum1 - sum2)/A(i,i);
    end

    if(times>=max)
        return;
    end
end
% 输出迭代次数和结果
disp(times);
disp(xn);

超松弛迭代法（Successive Over Relaxation Method）

分析

  超松弛迭代法，SOR，是对于高斯赛德尔迭代法的改进。它的关键之处在于松弛因子$\omega$，这个因子可以控制收敛的方向来控制迭代速度和迭代精度。由于迭代速度和迭代精度是相互矛盾的，如果我想得到更快的迭代速度（倾向于向新的x靠近），那么我就有可能偏离了我的正确值；如果我追求迭代精度（倾向于向旧的x靠近）那么，我的迭代速度就很慢。松弛因子$\omega$就是用来调节这两者的，务求找到一个平衡点。这里直接给出SOR的计算方法。
$$
\begin{cases}
x^{(0)} = (x_1^{(0)},x_2^{(0)},…,x_n^{(0)})^T，初始向量 \
x_i^{(k+1)} = x_i^{(k)} + \omega(b_i - \sum_{j=1}^{i-1}a_{ij}x_j^{(k+1)} - \sum_{j=i}^na_{ij}x_j^{(k)}) / a_{ii},\
i = 1,2,…,n; k=0,1,…表示迭代次数,\
\omega 为松弛因子\
\end{cases}
$$
使用SOR的时候，需要注意的是矩阵A必须是对称正定矩阵，同时$0 \lt \omega \lt 2 $。

代码实现

Matlab代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
% 超松弛迭代法
function[xn,times]=SOR(A,b,w,max)
n=size(A,1);
eps = 0.00001; % 精度控制
% 最大迭代次数
if nargin == 3
    max = 200;
end
%初始化向量
x0=zeros(n,1);
xn=zeros(n,1);
x0(1)=1;

times = 0; % 迭代次数
while norm(xn-x0)>=eps && times <= max
    times=times+1;
    x0=xn;

    for i=1:n
        sum1 = 0;
        sum2 = 0;
        for j =1:i-1
                sum1 = sum1 + A(i,j) * xn(j);
        end
        for j=i:n
            sum2 = sum2 + A(i,j) * x0(j);
        end
    xn(i)=x0(i) + w * (b(i) - sum1 - sum2)/A(i,i);
    end

    if(times>=max)
        return;
    end
end

% 输出迭代次数与结果
disp(times);
disp(xn);

共轭梯度法（Conjugate Gradient Method）

分析

  谈到共轭梯度法，首先要了解与线性方程组等价的变分问题。
设$A=(a_{ij})\in R^{n \times n}$是对称正定矩阵，$b =(b_1, b_2, \cdots, b_n)^T$，求解的线性方程组为Ax=b。考虑如下定义的二次函数$$\varphi(x) = \frac12(Ax,x) - (b,x)$$，该函数等价于对应的线性方程组。
性质1： 对一切$x\in R^n, \varphi(x)$的梯度为
$$\nabla \varphi(x) = Ax - b$$
性质2： 对一切$x,y\in R^n$及$\alpha \in R$，
$$
\varphi(x+\alpha y) = \frac12(A(x+\alpha y),x+\alpha y) - (b,x+\alpha y) \ = \varphi(x)+\alpha(Ax-b,y)+\frac{\alpha^2}{2}(Ay,y)
$$
性质3：设$x^* = A^{-1}b$是线性方程组Ax=b的解，则
$$
\varphi(x^*)=-\frac12(b,A^{-1}b) = -\frac12(Ax^*,x^*)
$$,
且对一切$x\in R^n$，有
$$
\varphi(x) - \varphi(x^*) = \frac12(Ax,x) - (Ax^*,x) + \frac12(Ax^*, x^*) \ = \frac12(A(x-x^*),x-x^*）
$$

根据上述二次函数的性质，我们可以知道，当$x^*$为令$\varphi(x)$最小时，$x^*$是该方程的解。这样，我们就把求解矩阵的问题转化为求解二次函数极小值点的问题

共轭梯度法的思想是，对于初始的一个x，使用方向$p^{(0)},p^{(1)},…,p^{(k-1)}$进行k次搜索，求得$x^{(k)}$，然后确定$p^{(k)}$的方向，这样能使x^{(k+1)}更快地求得$x^*$。其主要迭代公式为：
$$
x^{(k+1)} = x^{(k)} + \alpha_kp^{(k)}, \
x^{(k)} = \alpha_0p^{(0)} + \alpha_1p^{(1)} + \cdots + \alpha_{k-1}p^{(k-1)}。
$$
\alpha_k的值可以根据如下公式计算：
因为我们每步的求解过程中，都需要基于当前的x，求出下一个极小值，即
$$
\varphi(x^{(k+1)}) = \min_{\alpha \in R}\varphi(x^{(k)} + \alpha p^{(k)})
$$，
由于
$$
\varphi(x^{(k)} + \alpha p^{(k)}) = \varphi(x^{(k)}) + \alpha(Ax^{(k)}-b, p^{(k)}) + \frac{\alpha^2}{2}(Ap^{(k)},p^{(k)})
$$，
对上式求导，求出极小值
$$
\frac{d\varphi(x^{(k)} + \alpha p^{(k)})}{d \alpha} = (Ax^{(k)} - b, p^{(k)}) + \alpha(Ap^{(k)}, p^{(k)}) = 0,
$$
解得
$$
\alpha_k = -\frac{(Ax^{(k)} - b, p^{(k)})}{(Ap^{(k)},p^{(k)})}
$$
又因为我们希望$p^{(k)}$能使$x^{(k+1)}$能够更快地求得$x^*$，因此我们有
$$
\varphi(x^{(k+1)}) = \min_{x\in span{ p^{(0)},p^{(1)},\cdots,p^{(k)} }}\varphi(x)
$$,
然后我们把x分解成$x=y+\alpha p^{(k)}$，所以得到
$$
\varphi(x)=\varphi(y+\alpha p^{(k)} = \varphi(y) - \alpha(Ay, p^{(k)}) - \alpha(b,p^{(k)}) + \frac{\alpha^2}{2}(Ap^{(k)}, p^{(k)})
$$,
由于我们需要对x求导，又因为x用y来表示，所以对y求偏导。因为要为0，所以交叉项$(Ay,p^{(k)})$必须为0，这样一组向量p称为共轭向量。
以上就是对于共轭梯度法的核心思想的分析。下面直接给出算法：
（1）任取初始向量$x^{(0)}$，一般取为0，计算$r^{(0)} = b-Ax^{(0)$，取$p^{(0)}} = r^{(0)}$.
(2)对$k=0,1,\cdots,$计算
$$
\alpha_k = \frac{(r^{(k)},r^{(k)})}{(p^{(k)}, Ap^{(k)})} \
x^{(k+1)} = x^{(k)} + \alpha_kp^{(k)} \
r^{(k+1)} = r^{(k)} - \alpha_kAp^{(k)}, \beta_k = \frac{(r^{(k+1)},r^{(k+1)})}{(r^{(k)},r^{(k)})} \
p^{(k+1)} = r^{(k+1)} + \beta p^{(k)}
$$
(3)若$r^{(k)}=0$，或$(p^{(k)}, Ap^{(k)}) = 0$，则计算停止，得出结果。
这就是共轭梯度法的简要算法分析。

代码实现

Matlab代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
% 共轭梯度法
function[x] = CG(A,b,max)
% 初始化向量
n = size(A,1);
x0 = zeros(n,1);
r0=b-A*x0;
p0=r0;

% 最大迭代次数
if nargin == 2
    max = 200;
end

eps = 1.0e-6; % 精度控制
times = 0; % 迭代次数
while 1
    if ((abs(p0) < eps))
        break;
    end
    if (times > max)
        break;
    end
    times = times + 1;
    a0 = (r0' * r0) / (p0' * A*p0);
    x1 = x0 + a0*p0;

    r1 = r0 - a0*A*p0;

    b0 = (r1'*r1)/(r0'*r0);

    p1 = r1 + b0 *p0;


    x0 = x1;
    r0 = r1;
    p0 = p1;
end
x = x0;
end

小结

四个算法的时间比较

对比四种算法对同一个矩阵的求解计算时间：

n = 10
| 方法 | 时间 |
|:—-:|:—-:|
| 雅可比迭代法 | 0.0002|
| 高斯赛德尔迭代法 |0.0003|
| SOR迭代法 |0.0003|
| 共轭梯度法 |0.0001|

n = 100
| 方法 | 时间 |
|:—-:|:—-:|
| 雅可比迭代法 | 0.0053|
| 高斯赛德尔迭代法 |0.0044|
| SOR迭代法 |0.0048|
| 共轭梯度法 |0.0040|

n = 200
| 方法 | 时间 |
|:—-:|:—-:|
| 雅可比迭代法 | 0.0254|
| 高斯赛德尔迭代法 |0.0128|
| SOR迭代法 |0.0120|
| 共轭梯度法 |0.0036|

可以看出，迭代法的计算速度普遍较快，尤其是计算高维矩阵的时候，优势更加明显。其中，共轭梯度法的计算速度最快。

$\omega$对迭代速度的影响

这个测试是为了研究不同的$\omega$对SOR的速度的影响。这里采用测量迭代次数的方法，即对于不同omega，看看哪个算法的误差小于某个指定的值，记录当时的迭代次数，对于每次迭代我给了最高的迭代次数500。
结果如下：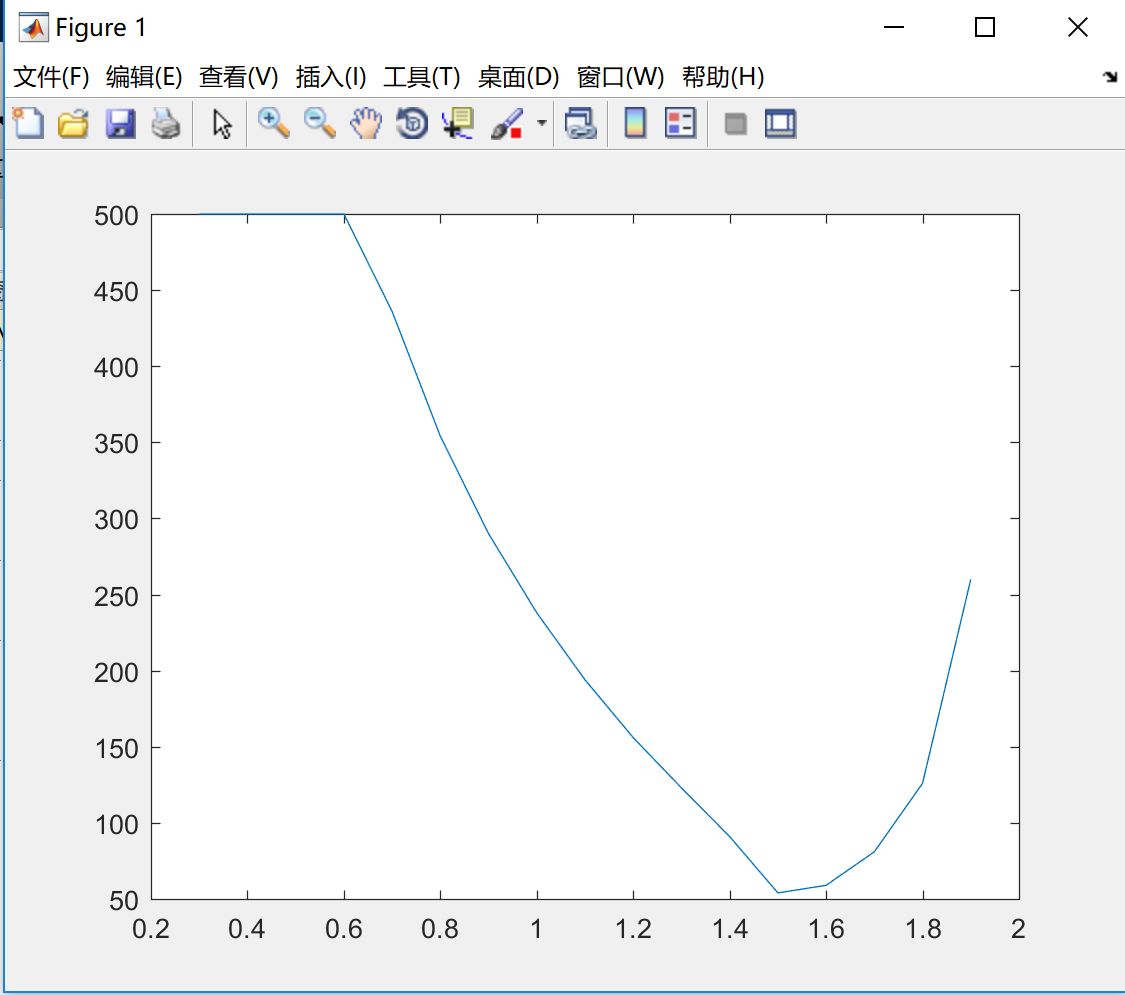
松弛因子测试
从图中可以看出，对于测试用的这个矩阵，最佳的松弛因子$\omega$约为1.5。对于不同的矩阵，最佳松弛因子是不同的。

  以上就是四种求解大型稀疏矩阵的迭代法的分析与实现，同时我也对算法的性能做出了简单的评估，谢谢！

参考资料：

1.数值分析（第5版） 李庆扬，王能超，易大义 *编

Welcome to my other publishing channels