贝叶斯分类器

Intro

贝叶斯分类器是机器学习算法中非常重要的一个算法，它是基于朴素贝叶斯理论的。这篇博客中我将详细介绍贝叶斯分类器的由来，以及应用贝叶斯分类器做一个垃圾邮件过滤和新闻分类。

Github项目地址：https://github.com/leungyukshing/Machine-Learning/tree/master/Bayes

原理

基本思想

贝叶斯分类器对于分类问题一个最基本的思想是：谁的概率大就选谁。用数学语言描述，对于数据$(x,y)$，类别$P_1,P_2$：
$$
\begin{cases}
P_1(x, y) \gt P_2(x,y),该数据为类别1 \
P_1(x,y) \lt P_2(x, y),该数据为类别2
\end{cases}
$$
在了解贝叶斯分类器之前，我们先来了解几个关于概率的基本概念。

条件概率

大家对于条件概率应该非常熟悉，这里就直接给出例子说明。
$$
P(A|B) = \frac{P(A\cap B)}{P(B)}
$$
表示的是在事件B发生的情况下，事件A发生的概率。

我们根据上式进行推导：
$$
\because P(B|A) = \frac{P(A\cap B)}{P(A)} \
\therefore P(A\cap B) = P(A|B)P(B)=P(B|A)P(A)
\therefore P(A|B) = \frac{P(B|A)P(A)}{P(B)}
$$
这样我们借助了$P(A\cap B)$来建立了$P(A|B)$和$P(B|A)$之间的关系。

全概率公式

首先给出一条容易理解的等式：
$$
P(B) = P(B\cap A) + P(B \cap A^{‘})
$$
这条式子表示的是，B发生的概率由两部分组成：一个是A发生时B发生的条件概率，另一个是A不发生时B发生的条件概率。

然后我们用$P(B\cap A) = P(B|A)P(A)$替换，得到：
$$
P(B) = P(B|A)P(A) + P(B|A^{‘})P(A^{‘})
$$
这条就是全概率公式。它的含义为：若$A$和$A^{‘}$构成样本空间的一个划分，那么事件$B$的概率等于$A$和$A^{‘}$的概率分别乘以$B$对这两个事件的条件概率之和。

如果我们用全概率公式替换掉条件概率公式的分母，可以得到：
$$
P(A|B) = \frac{P(B|A)P(A)}{P(B|A)P(A) + P(B|A^{‘})P(A^{‘})}
$$

贝叶斯推断

我们重新来看条件概率的公式，稍微调整一下分子的顺序：
$$
P(A|B) = P(A)\cdot\frac{P(B|A)}{P(B)}
$$
这样看的话，公式就可以分成三部分：

$P(A)$：先验概率（prior probability），在事件$B$发生前，我们对事件$A$概率的一个判断。
$P(A|B)$：后验概率（posterior probability），在事件$B$发生后，我们对事件$A$概率的重新评估。
$\frac{P(B|A)}{P(B)}$：可能性函数（likelihood），一个调整因子，使得预估概率更接近真实的概率。我们来看看这个可能性函数的作用：
- $\frac{P(B|A)}{P(B)} \lt 1$：先验概率被削弱，事件$A$可能性变小；
- $\frac{P(B|A)}{P(B)} = 1$：事件$B$无助于判断事件$A$的可能性；
- $\frac{P(B|A)}{P(B)} \gt 1$：先验概率被增强，事件$A$可能性变大。

我们用一个例子来说明这些概念的作用。假设现在有两个一模一样的箱子，第一个箱子中有30个黑球，10个白球；第二个箱子中有20个黑球，20个黑球。请问，从两个箱子中摸出了一个球，确定是黑球，那么这个黑球来自第一个箱子的概率有多大？

我们定义$P(H_1),P(H_2)$分别为从第一个箱子和第二个箱子取出球的概率。可以知道，$P(H_1)=P(H_2)=0.5$。这个就是先验概率。然后我们定义$P(E)$为取出黑色球的概率。这样就能够根据上面写的公式来表示我们要求的概率了：
$$
P(H_1|E)=P(H_1)\frac{P(E|H_1)}{P(E)} = \frac{P(H_1)\cdot P(E|H_1)}{P(E|H_1)P(H_1) + P(E|H_2)P(H_2)} = \frac{0.5 \times 0.75}{0.75 \times 0.5 + 0.5 \times 0.5} = 0.6
$$
也就是说，取出黑球这个事件增强了从第一个箱子取出黑球的可能性，即先验概率被增强了。

朴素贝叶斯

朴素贝叶斯和上面的概念是完全不一样的，它的主要内容是：对条件各概率分布做了条件独立性的假设，即条件之间是相互独立的。假设有$n$个特征，那么有：
$$
\begin{aligned}
P(a|X) &= P(X|a)P(a)=P(x_1, x_2,x_3,\cdots,x_n|a)P(a) \
&= {p(x_1|a) \times p(x_2|a) \times p(x_3|a) \times \cdots \times p(x_n|a)}p(a)
\end{aligned}
$$
把各个条件独立分开对于计算是非常有好处的，这也是贝叶斯分类器可以实现的统计学基础。

贝叶斯分类器

基于朴素贝叶斯的思想，贝叶斯分类器的基本方法是：在统计资料的基础上，依据某些特征，计算各个类别的概率，从而实现分类。

实战

垃圾邮件过滤

垃圾邮件过滤是机器学习的经典应用场景。这里利用贝叶斯分类器对邮件进行过滤。数据源：https://github.com/leungyukshing/Machine-Learning/tree/master/Bayes/email

邮件文本预处理

我们需要对邮件文本进行预处理，将文本切分成单词，然后使用所有的单词去构建起一个词典。我们的目的是根据单词去判断一个邮件是否垃圾邮件。

import re
def textParse(bigStr):
    listOfTokens = re.split(r'\W*', bigStr)
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]

def createVocabList(dataSet):
    vocabSet = set([])
    for document in dataSet:
        vocabSet = vocabSet | set(document)
    return list(vocabSet)

文本向量化

我们拥有了词典，但是在计算概率的过程中使用字符串还是比较复杂，因此我们需要将文本向量化——即用一个向量来表示一个文本，向量每个元素对应字典里面的每个单词，如果这个单词在该文本中出现了，那么在向量的对应位置上就为1，否则为0。

import numpy as np
import random

def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else:
            print('the word: %s is not in my Vocabulary!' % word)
    return returnVec

计算概率

现在我们来看看整个分类问题的核心是什么：
$$
P(类别|{单词1，单词2 \cdots ，单词n}) = {P(单词1|类别) \times P(单词2|类别) \times P(单词3|类别) \times \cdots \times P(单词n|类别)}P(类别)
$$
这个类别对应了就是邮件的类别（0为正常邮件，1为垃圾邮件）。对于每一个训练集来说，邮件的类别是已知的，我们可以根据计算文本向量每个位置的概率，从而得到后面一系列的条件概率，最终算出来要求的这个概率。

先看代码，然后再逐步分析：

def trainNB0(trainMatrix, trainCategory):
    numberOfTrainDocs = len(trainMatrix) # 训练样本数
    numberOfWords = len(trainMatrix[0]) # 文本向量长度
    pAbusive = sum(trainCategory) / float(numberOfTrainDocs) # P(垃圾邮件)
    # 拉普拉斯平滑
    p0Num = np.ones(numberOfWords)
    p1Num = np.ones(numberOfWords)
    p0Denom = 2.0
    p1Denom = 2.0

    for i in range(numberOfTrainDocs):
        # 分类别计算
        if trainCategory[i] == 1:
            # 垃圾邮件
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            # 正常邮件
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])

    p0Vect = np.log(p0Num / p0Denom) # P(每个单词|正常邮件)
    p1Vect = np.log(p1Num / p1Denom) # P(每个单词|垃圾邮件)
    return p0Vect, p1Vect, pAbusive

这里就是计算上述公式中右边部分的代码。p1Num统计的是在已知垃圾邮件的情况下，各单词的出现次数，是一个向量。p1Denom统计的是所有垃圾邮件单词的总数量，两个的比值是一个向量，里面存放着就是垃圾邮件的条件概率，即$P(每个单词|垃圾邮件)$。

为什么计算条件概率的时候初始化不是初始化为0呢？我们还是看回公式：
$$
P(类别|{单词1，单词2，\cdots ，单词n}) = {P(单词1|类别) \times P(单词2|类别) \times P(单词3|类别) \times \cdots \times P(单词n|类别)}P(类别)
$$
如果某一个单词的条件概率为0，即$P(单词x|类别) = 0$，那么就会导致整条式子为0。也就是说，在实际应用中，如果有些单词的条件概率为0或者很小，我们这个方法就行不通了。

于是我们进行微处理——拉普拉斯平滑（Laplace Smoothing）。它是比较常见的平滑方法，做法就是将分子初始化为1，分母初始化为2。

上面提到实际应用中，精度问题也是必须考虑的问题之一，如果这些条件概率很小，那么相乘之后就会有精度问题。这里的处理是用一个对数的方法，避免精度产生的问题。

测试

我们将所有的数据（共50份）分为两部分，40个训练集，10个测试集。然后使用训练集构建贝叶斯分类器，对10个测试样例进行测试，最后得到结果。

def spamTest():
    docList = []; # 文本数组
    classList = []; # 类型数组（0，1）
    fullText = []
    # 读取数据
    for i in range(1, 26):
        wordList = textParse(open('email/spam/%d.txt' % i, 'r').read())
        docList.append(wordList)
        fullText.append(wordList)
        classList.append(1)
        wordList = textParse(open('email/ham/%d.txt' % i, 'r').read())
        docList.append(wordList)
        fullText.append(wordList)
        classList.append(0)
    vocabList = createVocabList(docList) #创建词汇表

    trainingSet = list(range(50)) # 训练集下标
    testSet = [] # 测试集下标
    # 随机挑选10个样例作为测试集
    for i in range(10):
        randIndex = int(random.uniform(0, len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del(trainingSet[randIndex]) # 在训练集中删除

    trainMat = [] # 训练集矩阵
    trainClasses = [] # 训练集标签向量
    # 构建训练集
    for docIndex in trainingSet:
        trainMat.append(setOfWords2Vec(vocabList, docList[docIndex])) # 文本向量化
        trainClasses.append(classList[docIndex])

    p0V, p1V, pSpam = trainNB0(np.array(trainMat), np.array(trainClasses)) # 训练朴素贝叶斯模型

    # 测试部分
    errorCount = 0
    for docIndex in testSet:
        wordVector = setOfWords2Vec(vocabList, docList[docIndex]) # 文本向量化
        if classifyNB(np.array(wordVector), p0V, p1V, pSpam) != classList[docIndex]:
            errorCount += 1
            print("Bad Cases：",docList[docIndex])
    print('Error Rate：%.2f%%' % (float(errorCount) / len(testSet) * 100))


if __name__ == '__main__':
    spamTest()

结果

最终的测试结果是比较好的，基本都在10%以内，大多数情况下都能完全分类正确。

新闻分类

除了上面应用在垃圾邮件分类上，贝叶斯分类器还能用在新闻分类中。原理是很相似的，也是根据词语的不同来计算条件概率。这里我们尝试对中文文本进行分类，而且类别也相应地增加。

数据集：https://github.com/leungyukshing/Machine-Learning/tree/master/Bayes/SogouC

新闻文本预处理

我们处理的是中文文本，所以需要先对文本进行读取和切分，这里用到了一个中文分词的库——jieba。类似地，我们也是通过构建词典来将文本向量化。

def TextProcessing(folder_path, test_size = 0.2):
    folder_list = os.listdir(folder_path)
    data_list = [] # 文本数组
    class_list = [] # 类别数组

    for folder in folder_list:
        new_folder_path = os.path.join(folder_path, folder)
        files = os.listdir(new_folder_path)

        j = 1
        for file in files:
            if j > 100:
                break
            with open(os.path.join(new_folder_path, file), 'r', encoding='utf-8') as f:
                raw = f.read()
            # 分词
            word_cut = jieba.cut(raw, cut_all=False)
            word_list = list(word_cut)

            data_list.append(word_list)
            class_list.append(folder)
            j += 1
        #print(data_list)
        #print(class_list)
    # 将文本和类别压缩处理
    data_class_list = list(zip(data_list, class_list))
    random.shuffle(data_class_list) # 随机打乱

    # 根据测试集比例test_size划分训练集和测试集
    index = int(len(data_class_list) * test_size) + 1
    train_list = data_class_list[index:]
    test_list = data_class_list[:index]
    # 分别解压
    train_data_list, train_class_list = zip(*train_list)
    test_data_list, test_class_list = zip(*test_list)

    # 用训练集构建词典
    all_words_dict = {}
    for word_list in train_data_list:
        for word in word_list:
            if word in all_words_dict.keys():
                all_words_dict[word] += 1
            else:
                all_words_dict[word] = 1

    # 根据词语的词频排序，从高到低
    all_words_tuple_list = sorted(all_words_dict.items(), key=lambda f: f[1], reverse=True)
    # 解压出词典
    all_words_list, all_words_nums = zip(*all_words_tuple_list)
    all_words_list = list(all_words_list)
    return all_words_list, train_data_list, test_data_list, train_class_list, test_class_list


if __name__ == '__main__':
    folder_path = './SogouC/Sample'
    all_words_list, train_data_list, test_data_list, train_class_list, test_class_list = TextProcessing(folder_path, test_size = 0.2)
    print(all_words_list)

这里数据集已经给出了常见的结束词语，我们需要在字典中去除掉这些词语，首先构建出结束词语的词典。

# 构建结束词语集合
def makeWordsSet(words_file):
    words_set = set()
    with open(words_file, 'r', encoding='utf-8') as f:
        for line in f.readlines():
            word = line.strip()
            if len(word) > 0:
                words_set.add(word)
    return words_set

精简词典

上面的步骤就和垃圾邮件过滤一样，提取出来了所有的词语，构成了一个词典。但是这个词典的好坏对于结果的影响是非常重大的。我们可以print一下，发现这个词典中大量的高频词都是一些无实际意义的词语，如“在”、“了”、”很“。这些助词、介词对于文本的分类并没有实质的作用，因此我们需要把这些无意义的高频词去除掉，否则将严重影响分类结果。

处理的原则有三个：

去除数字
去除在结束词语列表中的词语
去除长度过短或过长的词语

'''
    构建词典，去除部分高频词、结束词语集合
    deleteN: 去除高频词的个数
    stopwords_set: 结束词语集合
'''
def words_dict(all_words_list, deleteN, stopwords_set = set()):
    feature_words = []
    n = 1
    for t in range(deleteN, len(all_words_list), 1):
        if n > 1000:
            break
        # 除去数字、结束词语、长度适中
        if not all_words_list[t].isdigit() and all_words_list[t] not in stopwords_set and 1 < len(all_words_list[t]) < 5:
            feature_words.append(all_words_list[t])
        n += 1
    return feature_words

文本向量化

这里的文本向量化思想与垃圾邮件分类是一样的。

def TextFeatures(train_data_list, test_data_list, feature_words):
    def text_features(text, feature_words):
        text_words = set(text)
        features = [1 if word in text_words else 0 for word in feature_words]
        return features
    train_feature_list = [text_features(text, feature_words) for text in train_data_list]
    test_feature_list = [text_features(text, feature_words) for text in test_data_list]
    return train_feature_list, test_feature_list

构建贝叶斯分类器

上面我们自己实现了贝叶斯分类器，这里我们试一下使用sklearn提供的贝叶斯分类器。

from sklearn.naive_bayes import MultinomialNB

def TextClassifier(train_feature_list, test_feature_list, train_class_list, test_class_list):
    classifier = MultinomialNB().fit(train_feature_list, train_class_list)
    test_accuracy = classifier.score(test_feature_list, test_class_list)
    return test_accuracy

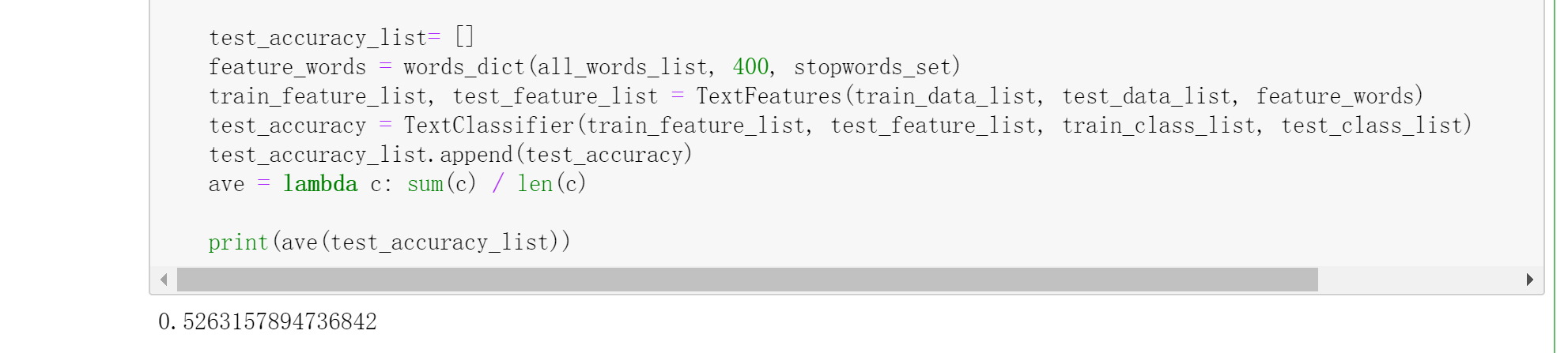
测试及优化

if __name__ == '__main__':
    folder_path = './SogouC/Sample'
    all_words_list, train_data_list, test_data_list, train_class_list, test_class_list = TextProcessing(folder_path, test_size = 0.2)

    stopwords_file = './stopwords_cn.txt'
    stopwords_set = makeWordsSet(stopwords_file)

    test_accuracy_list= []
    feature_words = words_dict(all_words_list, 400, stopwords_set)
    train_feature_list, test_feature_list = TextFeatures(train_data_list, test_data_list, feature_words)
    test_accuracy = TextClassifier(train_feature_list, test_feature_list, train_class_list, test_class_list)
    test_accuracy_list.append(test_accuracy)
    ave = lambda c: sum(c) / len(c)

    print(ave(test_accuracy_list))

我们可以运行测试，看到结果：

注意我之前提到过，词典的质量影响着分类的准确度，这里删掉前400个高频词（是随便调的一个参数），那么比较好的是deleteN是多少呢？我们可以自己写一个循环去找到这个最优参数。

if __name__ == '__main__':
    folder_path = './SogouC/Sample'
    all_words_list, train_data_list, test_data_list, train_class_list, test_class_list = TextProcessing(folder_path, test_size = 0.2)

    stopwords_file = './stopwords_cn.txt'
    stopwords_set = makeWordsSet(stopwords_file)

    test_accuracy_list= []
    deleteNs = range(0, 1000, 20)
    for deleteN in deleteNs:
        feature_words = words_dict(all_words_list, deleteN, stopwords_set)
        train_feature_list, test_feature_list = TextFeatures(train_data_list, test_data_list, feature_words)
        test_accuracy = TextClassifier(train_feature_list, test_feature_list, train_class_list, test_class_list)
        test_accuracy_list.append(test_accuracy)

    plt.figure()
    plt.plot(deleteNs, test_accuracy_list)
    plt.title('deleteN and test_accuracy')
    plt.xlabel('deleteN')
    plt.ylabel('Accuracy')
    plt.show()

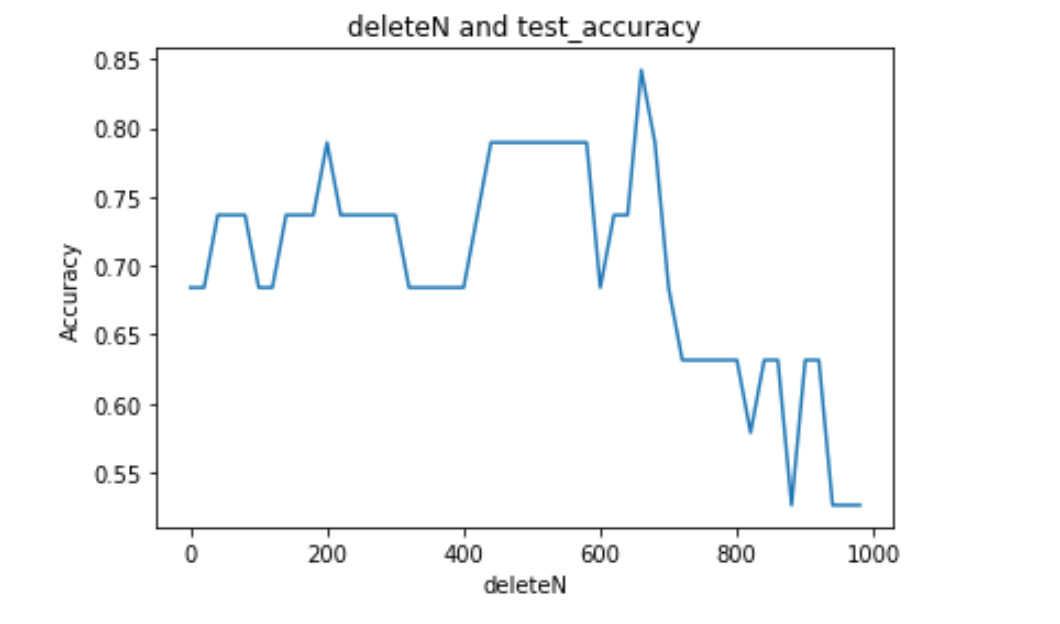
我从0一直到1000，以步长为20去搜索这个最优的deleteN，输出deleteN-Accuracy曲线：

从图中可以大致看出，最优的deleteN应该是在600-700之间。所以调整参数为680，再次测试：

总结

至此，我就把贝叶斯分类器的一些基础知识分享给大家了，借用了两个实例来应用了一下贝叶斯分类器（既有自己实现的，也有调用sklearn的）。相信通过这篇博客，大家贝叶斯分类器有了一定了解。欢迎提出宝贵的意见，谢谢您的支持！