LeetCode解题报告（193）-- 133. Clone Graph

Problem

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

For simplicity sake, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:

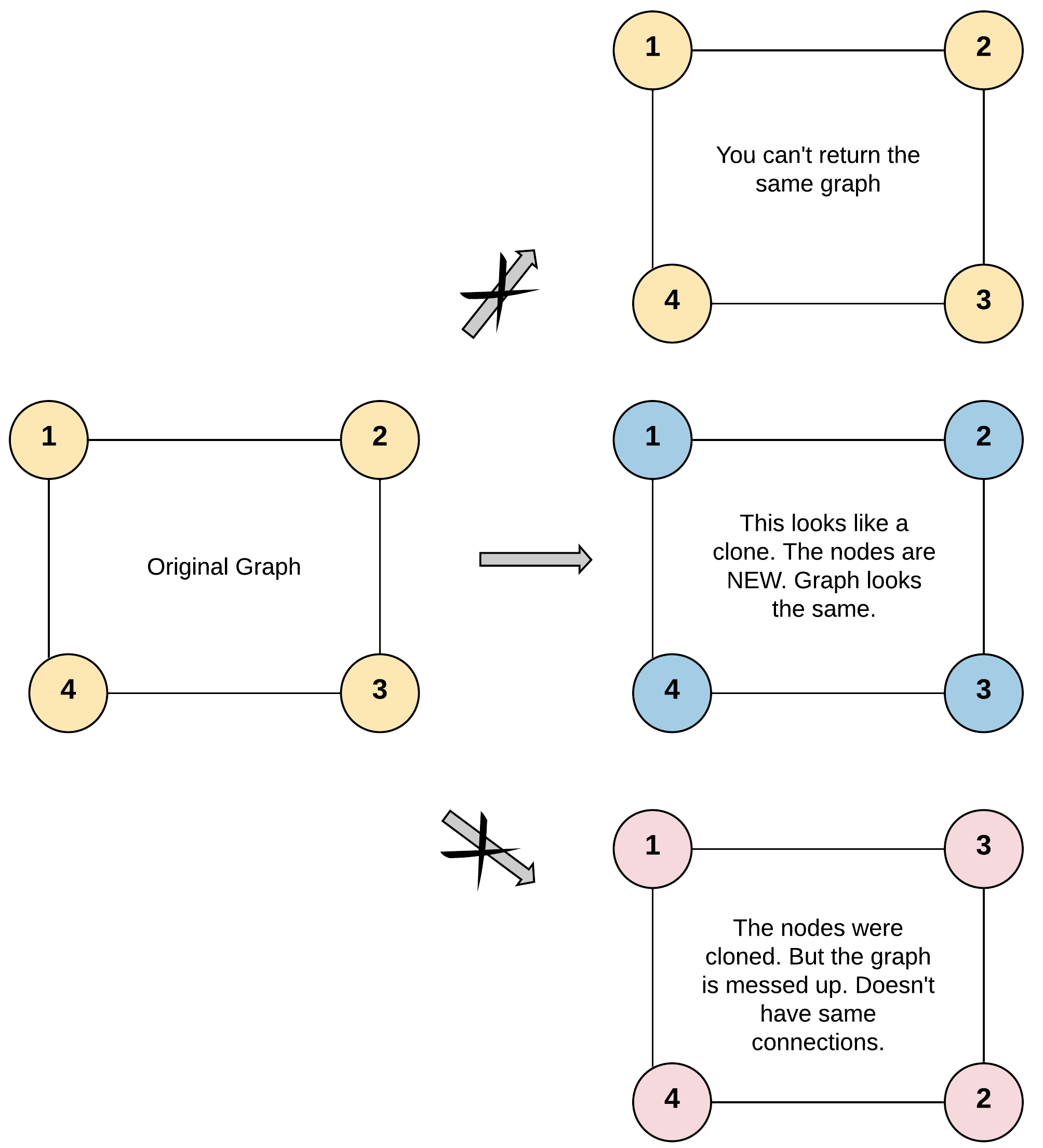
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

1
2
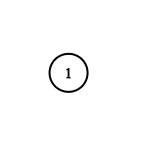
3

Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

1
2
3

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Example 4:

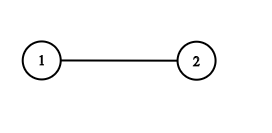
1 2	Input: adjList = [[2],[1]] Output: [[2],[1]]

Constraints:

1 <= Node.val <= 100
Node.val is unique for each node.
Number of Nodes will not exceed 100.
There is no repeated edges and no self-loops in the graph.
The Graph is connected and all nodes can be visited starting from the given node.

Analysis

题目要求我们对一个图进行深复制。要复制肯定就要遍历，图的遍历主流是DFS或者BFS，DFS是比较简单的，因为用递归实现比较方便。

在遍历的过程中，每到一个节点，就创建该节点newNode，然后从它的neighbors找下一个节点。下一个节点创建好之后，也要放回到newNode的neighbors中。这里需要注意重复的问题，我们需要记录下已经创建过的节点。其余的就没什么难度了。

Solution

记录已经创建过的节点，本来用一个set就可以实现了。但是，因为我们要的是复制，而不是遍历，所以已经创建过的节点也要放到neighbors中，所以比较好的做法是用一个map来存，记录原图的节点和新图的节点之间的对应关系。

Code

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/

class Solution {
public:
    Node* cloneGraph(Node* node) {
        unordered_map<int, Node*> visited;
        return helper(node, visited);
    }
private:
    Node* helper(Node* node, unordered_map<int, Node*>& visited) {
        if (!node) {
            return NULL;
        }
        if (visited.count(node->val)) {
            return visited[node->val];
        }
        Node* newNode = new Node(node->val);
        visited[node->val] = newNode;
        for (auto neighbor: node->neighbors) {
            newNode->neighbors.push_back(helper(neighbor, visited));
        }
        return newNode;
    }
};

Summary

这是一道比较常规的图的遍历问题，主要是利用递归做DFS。在面试中应该对这类题目非常熟悉。这道题目的分享到这里，谢谢！