Halo

A magic place for coding

0%

LeetCode解题报告（213）-- 1026. Maximum Difference Between Node and Ancestor

Posted on Edited on Valine:

Problem

Given the root of a binary tree, find the maximum value V for which there exist different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.

A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.

Example 1:

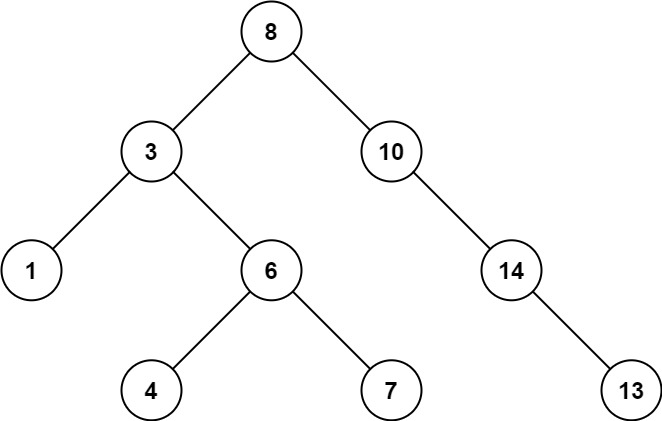
Example1

1
2
3
4
5
6
7
8
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Example 2:

Example2

1
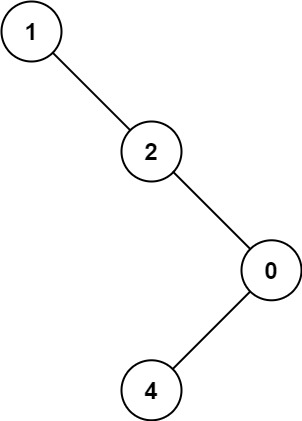
2
Input: root = [1,null,2,null,0,3]
Output: 3

Constraints:

  • The number of nodes in the tree is in the range [2, 5000].
  • 0 <= Node.val <= 105

Analysis

  这道二叉树的题目要求计算出两个节点最大的差的绝对值，同时要求这两个节点是父子关系。如果先不考虑第二个条件，做法就很简单了，对整棵树进行遍历，分别维护当前最大值和最小值，然后每个节点都去做差，保留最大的结果就是答案。

  但是有了第二条件，需要排除掉同级的情况。我在想需要用什么方法去解决这个问题，但是发现实际上遍历的方式就天然地解决了这个问题。上面说的维护当前最大值和最小值是对于某颗子树而言的，所以在左子树的最大值或最小值是不会影响右子树的，这样分析后问题就变得非常简单了。

Solution

  无

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxAncestorDiff(TreeNode* root) {
        if (!root) {
            return 0;
        }
        int result = 0;
        helper(root, root->val, root->val, result);
        return result;
    }
private:
    void helper(TreeNode* root, int maxValue, int minValue, int& result) {
        if (!root) {
            return;
        }

        result = max(result, max(abs(maxValue - root->val), abs(minValue - root->val)));
        maxValue = max(maxValue, root->val);
        minValue = min(minValue, root->val);
        helper(root->left, maxValue, minValue, result);
        helper(root->right, maxValue, minValue, result);
    }
};

Summary

  这道二叉树的题目虽然背景有点特殊，但是实际coding起来是非常简单的。在使用前序遍历保证了最大值和最小值的作用范围后，找出最大的绝对值就非常简单。这道题目的分享到这里，谢谢！

Welcome to my other publishing channels