LeetCode解题报告（23）-- 11. Container With Most Water

Problem

Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

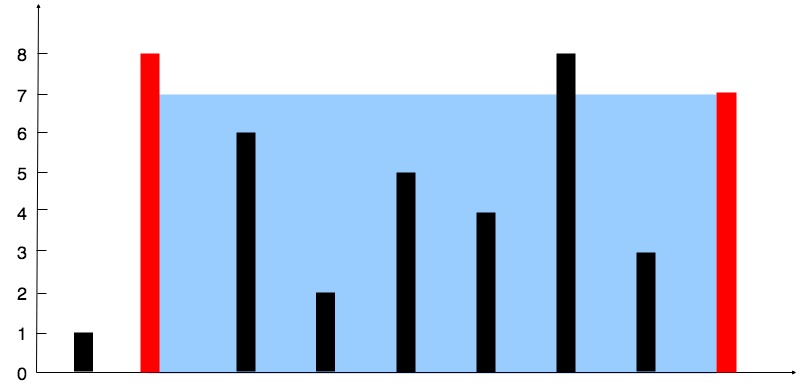
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example:

1 2	Input: [1,8,6,2,5,4,8,3,7] Output: 49

Analysis

这道题需要我们找出能够围成最大面积的两根柱子。第一种暴力做法就是双循环数组，找出每个组合所围成的面积，不断更新最大值就可以了，很显然这种算法的复杂度是$O(n^2)$。从第一个算法的过程中，我们可以知道，很多的组合都是无效的，即无法提供一个更大的面积，这些步骤是可以省去的，于是我想到了从两边开始遍历。那么如何保证这种方式能够得到最优解呢？由题目可知，每条边相隔1，也就是说，如果固定一条边，移动另一条边，如果移动的是较高的一条边，那么面积必定会减少（宽度减少，即使新边高度高于另一条边，总面积也必定减少）。基于这种推理，我们就可以移动更短的一条边来更新面积了，因为只有移动更短的一条边才有可能发现出更大的面积。

Solution

使用left和right两个下标，分别从数组的两端开始向中间遍历，每次移动较短的一个，不断更新最大值。

Code

class Solution {
public:
    int maxArea(vector<int>& height) {
        int maxValue = -1;
        int left = 0, right = height.size() - 1;
        int value;
        while (left != right) {
            value = (right - left) * min(height[left], height[right]);
            maxValue = (value > maxValue) ? value : maxValue;
            if (height[left] > height[right]) {
                right--;
            }
            else {
                left++;
            }
        }
        return maxValue;
    }
};

运行时间：约12ms，超过98.24%的CPP代码。

Summary

这道题要求解的话难度不大，但是要想到这样一个高效快速的算法还是有难度的。我的方法是在纸上多试几次，找出面积更新的规律。这道题的分析就到这里了，谢谢您的支持！