LeetCode解题报告（247）-- 1463. Cherry Pickup II

Problem

Given a rows x cols matrix grid representing a field of cherries. Each cell in grid represents the number of cherries that you can collect.

You have two robots that can collect cherries for you, Robot #1 is located at the top-left corner (0,0) , and Robot #2 is located at the top-right corner (0, cols-1) of the grid.

Return the maximum number of cherries collection using both robots by following the rules below:

From a cell (i,j), robots can move to cell (i+1, j-1) , (i+1, j) or (i+1, j+1).
When any robot is passing through a cell, It picks it up all cherries, and the cell becomes an empty cell (0).
When both robots stay on the same cell, only one of them takes the cherries.
Both robots cannot move outside of the grid at any moment.
Both robots should reach the bottom row in the grid.

Example 1:

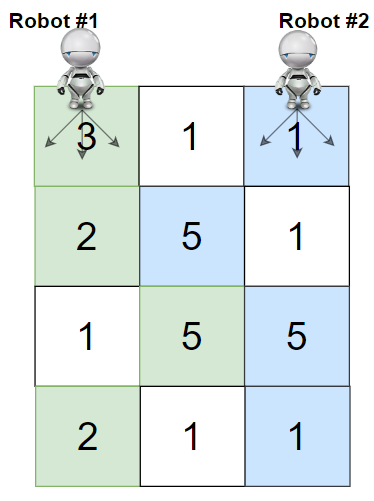
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
Output: 24
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.

Example 2:

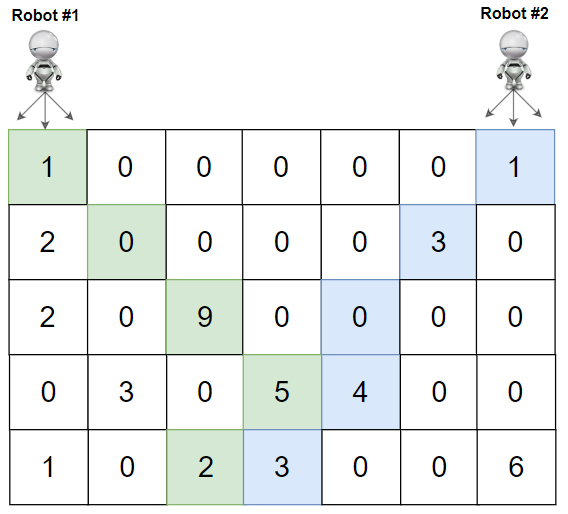
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Output: 28
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.

Example 3:

1 2	Input: grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]] Output: 22

Example 4:

1 2	Input: grid = [[1,1],[1,1]] Output: 4

Constraints:

rows == grid.length
cols == grid[i].length
2 <= rows, cols <= 70
0 <= grid[i][j] <= 100

Analysis

这是一道二维矩阵的题目，两个robot在上面走，走过的格子能够获得上面的cherries，问两个robots最多能获得多少个cherries。其中两个robot的移动方向只能是左下、正下、右下。首先要确定解题的思路，因为这里的总数每条路径是不同的，而且如果两个机器人走到同一个格子的话，只算一个机器人，所以这里一定要把整个流程走完，而且是两个机器人一起走。

确定好要遍历之后，先来看看每次移动的方向。每个机器人都有三个选择，所以两个机器人一共就有9种组合。对每一个组合都计算出结果，然后在所有的结果中挑选最大的，就是这一步能够获得的最多的cherries，所以这里就用到了递归。入参是位置，出参是获得的最大cherries的数量，再加上当前位置的cherries，就得到当前位置能够获得的最大的cherries了。

Solution

这道题目的思路并不复杂，就是递归遍历，难点在于如果把这个递归写的漂亮。首先入参是位置，所以位置信息需要传入，两个机器人各自的坐标一共四个值，但是因为两个机器人都是同时往下走，所以他的纵坐标是一样的，这里可以减少一个维度，只传3个。

同时，在使用递归的时候我们经常会遇到重复计算的问题，一般的解决方法就是用一个map或者数组去存放计算过的结果。这里是三个维度，所以用一个三维数组存计算过的结果，这样能够提高运算效率。

Code

class Solution {
public:
    int cherryPickup(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        memory = vector<vector<vector<int>>>(m, vector<vector<int>>(n, vector<int>(n, -1)));
        return helper(grid, 0, 0, n - 1);
    }
private:
    int helper(vector<vector<int>>& grid, int row, int col1, int col2) {
        if (memory[row][col1][col2] != -1) {
            return memory[row][col1][col2];
        }
        
        int res = grid[row][col1]; // robot1 pick up cherries
        if (col1 != col2) {
            res += grid[row][col2]; // robot2 pick up cherries
        }
        
        int maxResult = 0;
        // traverse different directions
        for (auto dir1: dirs) {
            int row_new = row + dir1[0], col_new1 = col1 + dir1[1];
            if (row_new == grid.size()) {
                break;
            }
            if (col_new1 < 0 || col_new1 == n) {
                continue;
            }
            for (auto dir2: dirs) {
                int col_new2 = col2 + dir2[1];
                if (col_new2 < 0 || col_new2 == n) {
                    continue;
                }
                
                maxResult = max(maxResult, helper(grid, row_new, col_new1, col_new2));
            }
        }
        
        res += maxResult;
        memory[row][col1][col2] = res;
        return res;
    }
    int m, n;
    vector<vector<vector<int>>> memory;
    int dirs[3][2] = {{1, -1}, {1, 0}, {1, 1}};
};

Summary

这道题目本质上还是一个遍历的问题，一般这种地图类的遍历会使用BFS/DFS，或者就是递归了。递归函数的出参一般都是答案，入参是位置信息，同时还要顾及到计算效率的问题。这道题目综合考察了coding的几个方面，非常值得总结。这道题目的分享到这里，谢谢您的支持！