LeetCode解题报告（276）-- 1329. Sort the Matrix Diagonally

Problem

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix’s end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

Example 1:

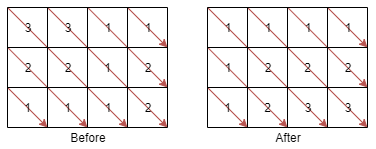
1 2	Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]] Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

1
2

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 100
1 <= mat[i][j] <= 100

Analysis

这道题目是给一个矩阵中的每一条对角线上的元素进行排序，第一次碰到这类题目有点不知所措。不妨先回退一个难度进行思考，如果要对一个矩阵中，每一行或者每一列进行排序呢？

如果只是对行或者列排序是比较简单的，我们只需要把每一行（列）放到一个数组中，然后进行排序，最后再赋值回去就可以了。

再回来看看这个题目，思路上应该也是把每个对角线的元素拿出来放到数组中，所以难点就变成了如何去处理每个对角线。题目的Hint中给了一个很重要的提示：使用i-j去定位到同一条对角线。这样一来问题就简单多了，遍历矩阵，然后我们用i - j + n去表示同一条对角线，把元素都放到一个vector中。然后再逐个进行排序，最后写回到矩阵中即可。

Solution

无

Code

class Solution {
public:
    vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
        const int m = mat.size();
        const int n = mat[0].size();
        vector<deque<int>> qs(m + n);
        for (int i = 0; i < m; ++i)
          for (int j = 0; j < n; ++j)
            qs[i - j + n].push_back(mat[i][j]);
        
        for (auto& q : qs)
          sort(begin(q), end(q));
        
        for (int i = 0; i < m; ++i)
          for (int j = 0; j < n; ++j) {
            mat[i][j] = qs[i - j + n].front();
            qs[i - j + n].pop_front();
          }
        return mat;
    }
};

Summary

这道题目是矩阵排序中一道比较有趣的变种，但基本的原理和思路都是一样的，仅需要通过一个变化就能够统一到正常的排序中。这道题这道题目的分享到这里，谢谢您的支持！