Halo

A magic place for coding

0%

LeetCode解题报告（279）-- 1631. Path With Minimum Effort

Posted on Edited on Valine:

Problem

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route’s effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

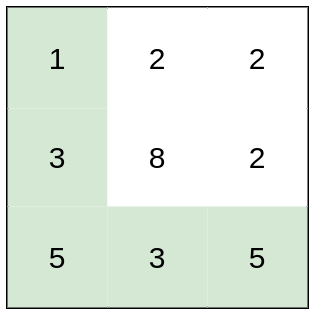
Example1

1
2
3
4
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

Example2

1
2
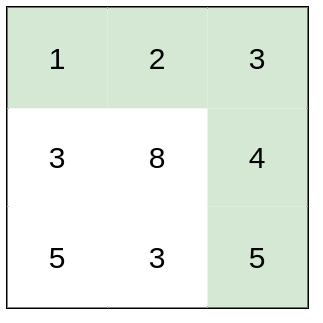
3
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

Example3

1
2
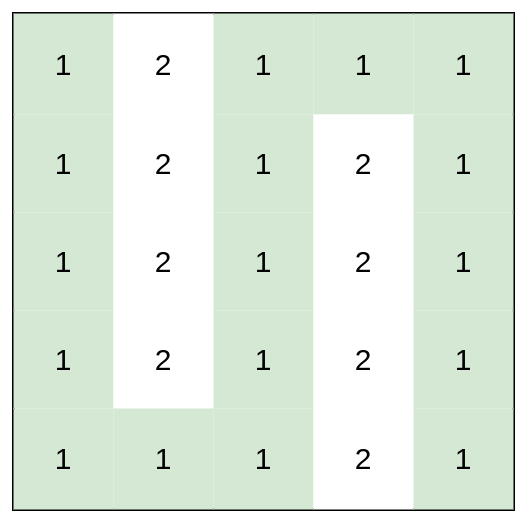
3
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

  • rows == heights.length
  • columns == heights[i].length
  • 1 <= rows, columns <= 100
  • 1 <= heights[i][j] <= 106

Analysis

  题目给出了一个矩阵，起点是左上角，终点是右下角，定义Effort为走过的路径中相邻元素的差的绝对值的最大值。要求是找到这个Effort的最小值，不需要求出整个路径。去维护每条路径的Effort是比较困难的，一个是因为路径很多，而且遇到分叉后这个值的维护也很困难，我们需要用另一种更加巧妙的方法去找到这个Effort。

  看回题目的要求，要找的是Effort的值，而不需要找到整条路径，我们可以从这个地方切入。从答案作为切入点，无论如何，最后答案的值如果不存在就是0，如果存在，一定会在一个范围中，这个范围就是[1, 1e6]。对于答案存在的情况，我们可以采用二分答案的方法来解决。把题目转化为能否找到一条路径，它的Effort等于k，然后我们不断二分这个k。

  判断某个能否找到一条路径的Effor为k这个问题就非常简单了，我们只需要每走一步的时候判断两个相邻位置的差的绝对值和k的关系，如果比k大，说明当前这条路径不符合要求，直接return false，二分法往前半部分继续搜索；如果走到终点都没有超过这个k，说明当前路径的Effort比k小，二分法往后半部分继续搜索。

Solution

  遍历的时候因为要避免环的出现，所以需要一个visited矩阵记录已经遍历过的位置。因为这里用的是BFS，用的是queue，里面存放的是坐标，所以是pair。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        m = heights.size();
        n = heights[0].size();
        
        int left = 0, right = 1e6 + 1;
        while (left < right) {
            int mid = (left + right) / 2;
            if (canReach(heights, mid)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
private:
    int m;
    int n;
    int dirs[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
    bool canReach(vector<vector<int>>& heights, int cost) {
        queue<pair<int, int>> q;
        vector<vector<int>> visited(m, vector<int>(n, 0));
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                visited[i][j] = 0;
            }
        }
        visited[0][0] = 1;
        q.emplace(0, 0);
        

        while (!q.empty()) {
            auto [cx, cy] = q.front();
            q.pop();
            if (cx == m - 1 && cy == n - 1) {
                return true;
            }
            for (int k = 0; k < 4; k++) {
                int dx = cx + dirs[k][0];
                int dy = cy + dirs[k][1];
                if (dx < 0 || dx == m || dy < 0 || dy == n) {
                    continue;
                }
                if (abs(heights[cx][cy] - heights[dx][dy]) > cost) {
                    continue;
                }
                if (visited[dx][dy]++) {
                    continue;
                }
                q.emplace(dx, dy);
            }
        }
        return false;
    }
};

Summary

  这道题目是难度比较大的一道综合类题目，包括了图的遍历以及二分答案这两个主要的算法知识点。图的遍历应该是比较循规蹈矩的，都是有模版可以参考。而二分答案是在算法题中非常常见的一种算法。这道题这道题目的分享到这里，谢谢您的支持！

Welcome to my other publishing channels