LeetCode解题报告（327)-- 417. Pacific Atlantic Water Flow

Problem

You are given an m x n integer matrix heights representing the height of each unit cell in a continent. The Pacific ocean touches the continent’s left and top edges, and the Atlantic ocean touches the continent’s right and bottom edges.

Water can only flow in four directions: up, down, left, and right. Water flows from a cell to an adjacent one with an equal or lower height.

Return a list of grid coordinates where water can flow to both the Pacific and Atlantic oceans.

Example 1:

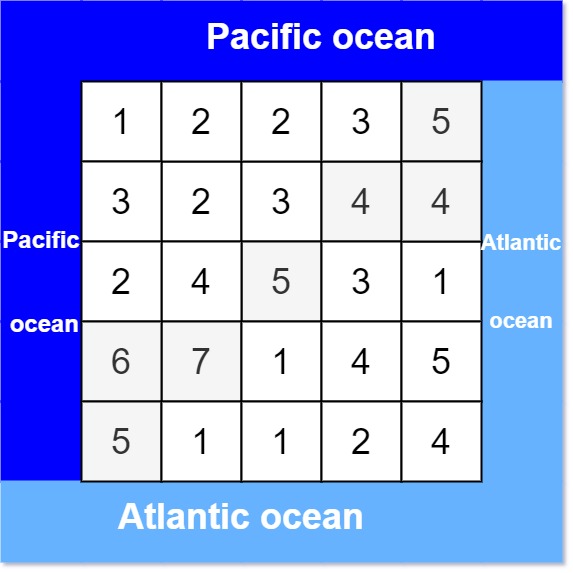
1 2	Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

Example 2:

1 2	Input: heights = [[2,1],[1,2]] Output: [[0,0],[0,1],[1,0],[1,1]]

Constraints:

m == heights.length
n == heights[i].length
1 <= m, n <= 200
1 <= heights[i][j] <= 105

Analysis

题目的本质是一个二维矩阵遍历的问题，题目的意思有点复杂。首先题目说左边和上边是太平洋，右边和下边是大西洋，每个位置上的数值是高度，遵循水往低处流的原则，问有哪些位置的水可以最终流入海洋。其实这个就是一个连通性问题，在矩阵中任意选一个点，连通的条件是当前位置的值比下一步位置的值要大（或等于），最后看看是否两个海洋都能到达即可。

这里涉及到一个复杂性的问题，原因是，如果要对矩阵中所有的位置都检查一遍，计算复杂度很高，而且会有很多重复计算的情况。我们不妨逆向思维，从四条边出发，反向寻找。从左边和上边出发，找到矩阵中能连通的点；同理，从右边和下边出发，也找到矩阵中能够连通的点，然后把这两个集合的点求一个交集即可。

Solution

需要注意，在反向处理时，连通的条件就变为当前位置的值必须要严格小于下一个位置的值。

Code

class Solution {
public:
    vector<vector<int>> pacificAtlantic(vector<vector<int>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) {
            return {};
        }
        vector<vector<int>> result;
        this->m = matrix.size();
        this->n = matrix[0].size();
        
        vector<vector<bool>> pacific(m, vector<bool>(n, false));
        vector<vector<bool>> atlantic(m, vector<bool>(n, false));
        
        for (int i = 0; i < this->m; i++) {
            dfs(matrix, pacific, INT_MIN, i, 0);
            dfs(matrix, atlantic, INT_MIN, i, this->n - 1);
        }
        
        for (int j = 0; j < this->n; j++) {
            dfs(matrix, pacific, INT_MIN, 0, j);
            dfs(matrix, atlantic, INT_MIN, this->m - 1, j);
        }
        
        for (int i = 0; i < this->m; i++) {
            for (int j = 0; j < this->n; j++) {
                if (pacific[i][j] && atlantic[i][j]) {
                    result.push_back({i, j});
                }
            }
        }
        return result;
    }
private:
    int m, n;
    
    void dfs(vector<vector<int>>& matrix, vector<vector<bool>>& visited, int pre, int i, int j) {
        if (i < 0 || i >= this->m || j < 0 || j >= this->n || visited[i][j] || matrix[i][j] < pre) {
            return;
        }
        
        visited[i][j] = true;
        dfs(matrix, visited, matrix[i][j], i + 1, j);
        dfs(matrix, visited, matrix[i][j], i - 1, j);
        dfs(matrix, visited, matrix[i][j], i, j + 1);
        dfs(matrix, visited, matrix[i][j], i, j - 1);
    }
};

Summary

这是一道比较简单的二维矩阵连通问题，其实原理还是DFS，只是需要变换一下遍历的方向。这道题目的分享到这里，感谢你的支持！