Halo

A magic place for coding

0%

LeetCode解题报告（348) -- 1074. Number of Submatrices That Sum to Target

Posted on Edited on Valine:

Problem

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

Example 1:

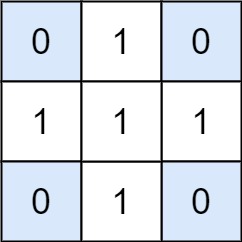
Example1

1
2
3
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

1
2
3
Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Example 3:

1
2
Input: matrix = [[904]], target = 0
Output: 0

Constraints:

  • 1 <= matrix.length <= 100
  • 1 <= matrix[0].length <= 100
  • -1000 <= matrix[i] <= 1000
  • -10^8 <= target <= 10^8

Analysis

  题目给出一个矩阵，还有一个目标值target，要求找出所有和为target的子矩阵的数量。暴力的解法是穷举出所有的子矩阵，然后每个都算一次和，与target值对比一下。这种做法最大的问题是重复计算了很多中间情况，那么优化的思路也很明显，我们把中间计算的结果存起来就好了。

  显然一下子处理矩阵的中间计算值不太好处理，我们先从一个维度开始，先计算每一行的中间值。我们对每一行做presum计算，即row[i]表示的是这一行区间[0,i]的所有数之和。有了每一行的presum之后，我们就能很方便地计算区间[i,j]的值，为row[j] - row[i - 1]。

  解决了每一行的问题，我们就可以来看矩阵的问题。我们只要限定左右边界，从上到下遍历，就能够计算出这个左右区间里面，从上到下矩阵的presum。但这个值我们就不需要再用一个数组去存了，可以直接存入map中，每次用sum - target看看是否在map中，如果在的话，说明符合要求的矩阵的数量+1。这里有点不好理解，举个例子，假设target = 1，如果从上到下矩阵的presum是[1,2,3,4]，那么在第一个的时候，sum - target = 0，同时把sum = 1存入map中；处理第二个的时候，sum - target = 1，在map中能找到，同时把sum = 2存入map中，以此类推，这样也算是在纵轴方向上的一个计算优化。

Solution

  需要特别注意，在限定左右边界时要注意边界情况。这里我为了便于理解，开presum数组时多开了一列，所以是某个区间的和是presum[col2] - presum[col1]。同时还要注意，map初始化的时候要预先存入<0,1>，这个是直接满足答案的条件。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> presum(m, vector<int>(n + 1, 0));
        
        for (int i = 0; i < m; i++) {
            for (int j = 1; j < n + 1; j++) {
                presum[i][j] = presum[i][j - 1] + matrix[i][j - 1];
            }
        }
        
        unordered_map<int, int> counter;
        int result = 0;
        for (int col1 = 0; col1 < n + 1; col1++) {
            for (int col2 = col1 + 1; col2 < n + 1; col2++) {
                counter = {{0, 1}};
                int temp = 0;
                for (int row = 0; row < m; row++) {
                    temp += presum[row][col2] - presum[row][col1];
                    result += counter.find(temp - target) != counter.end() ? counter[temp - target]: 0;
                    counter[temp]++;
                }
            }
        }
        return result;
    }
};

Summary

  这道题目难度比较大，主要的原理还是presum，只不过换成了二维的方式。主要的思路还是先求出每一行的presum，然后限定好左右边界，再从纵向presum求和处理。这道题目的分享到这里，感谢你的支持！

Welcome to my other publishing channels