LeetCode解题报告（355) -- 1192. Critical Connections in a Network

Problem

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

1
2
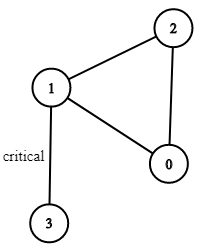
3

Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

Constraints:

1 <= n <= 10^5
n-1 <= connections.length <= 10^5
connections[i][0] != connections[i][1]
There are no repeated connections.

Analysis

题目给出了一个图，要求我们找到所有的critical边，对critical的定义是一旦删除这条边，某些节点就会失去和其他节点的连接。先理解一下题意，这里涉及到了连通分量的问题。critical边实际的意义就是，一旦移除，就会多一个连通分量。

一下子好像无从下手，我们先来看什么是连通分量。以Example1为例，如果用1作为起点，它有两条路（注意这里的每一步，不能往前一个点走，但是可以走访问过的点）：

往3走，然后就结束；
往0走，然后往2走，最后回到1，结束（或者是往2走，然后往0走，最后回到1，结束）。

对于1这个点来说，这两条路径是不一样的，第一条路实际上就是题目要找的critical边，而第二条路实际上是回环，并不存在critical边。所以我们的重点在于，如何去判断出第一条路径是有critical边，而第二条路径没有。

这里就要介绍一个图论中一个很重要的算法——Tarjan算法。这里我们不纠结于算法具体是什么或者完整实现是怎么样的，我们借助它的核心思路，然后直接来看应用到这道题上怎么做。其核心思想是基于深度优先解决图的连通性问题，这个点给了我很大的提示。我们要利用深度的信息去判断图的连通性，这个要怎么做呢？还是回到Example1中，还是用1作为起点，如果此时把1的深度定义为0，用DFS，那么它往后遍历每一个节点，深度就自增1。按照上面的两条路径：

节点3的深度是1，结束；
节点0的深度是1，节点2的深度是2，然后去到节点1的深度是0（这里不用更新为3，因为节点1的深度已经定义过了）。

根据这个深度我们能判断出来，如果dfs最后节点的深度大于当前的深度，则说明当前节点和最后的这个节点它们之间不能形成环，因此它们直接的connection就是critical的。这里需要注意dfs返回的结果是该节点往后的子孙节点中的最小深度。然后我们记录每一个节点的最小深度，如果已经访问过了，就不需要再做一遍dfs了。

Solution

无

Code

class Solution {
public:
    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
        vector<vector<int>> result;
        vector<int> depthArr(n, -1);
        vector<vector<int>> map(n, vector<int>());
        
        int size = connections.size();
        // construct connection map
        for (int i = 0; i < size; i++) {
            map[connections[i][0]].push_back(connections[i][1]);
            map[connections[i][1]].push_back(connections[i][0]);
        }
        
        dfs(0, 0, 0, map, depthArr, result);
        return result;
    }
    
private:
    int dfs(int current, int previous, int depth, vector<vector<int>> &map, vector<int> &depthArr, vector<vector<int>>& result) {
        depthArr[current] = depth;
        int minDepth = INT_MAX;
        
        
        for (int i: map[current]) {
            if (i == previous) {
                // not go back
                continue;
            }
            int endDepth;
            if (depthArr[i] == -1) {
                // not visited
                endDepth = dfs(i, current, depth + 1, map, depthArr, result);
                if (endDepth > depth) {
                    // the end point is deeper than the current point
                    // means that the current point is not in the circle
                    vector<int> temp;
                    temp.push_back(current);
                    temp.push_back(i);
                    result.push_back(temp);
                }
            } else {
                endDepth = depthArr[i];
            }
            minDepth = min(minDepth, endDepth);
        }
        return minDepth;
    }
};

Summary

这道题目是难度很大的图论题目，据说是亚麻的面试题。在做这道题目前确实在这方面没什么经验，这道题目提供了一个解决类似问题的思路，利用dfs来计算子孙节点的深度，通过深度来判断连通性。这道题目的分享到这里，感谢你的支持！