Halo

A magic place for coding

0%

LeetCode解题报告（391) -- 1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts

Posted on Edited on Valine:

Problem

You are given a rectangular cake of size h x w and two arrays of integers horizontalCuts and verticalCuts where:

  • horizontalCuts[i] is the distance from the top of the rectangular cake to the ith horizontal cut and similarly, and
  • verticalCuts[j] is the distance from the left of the rectangular cake to the jth vertical cut.

Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a large number, return this modulo 109 + 7.

Example 1:

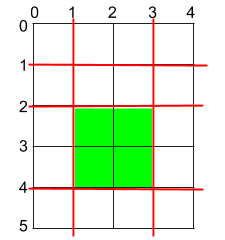
Example1

1
2
3
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
Output: 4 
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.

Example 2:

Example2

1
2
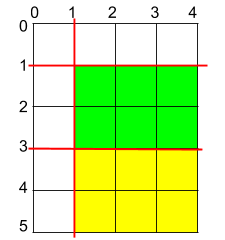
3
Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
Output: 6
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.

Example 3:

1
2
Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
Output: 9

Constraints:

  • 2 <= h, w <= 109
  • 1 <= horizontalCuts.length <= min(h - 1, 105)
  • 1 <= verticalCuts.length <= min(w - 1, 105)
  • 1 <= horizontalCuts[i] < h
  • 1 <= verticalCuts[i] < w
  • All the elements in horizontalCuts are distinct.
  • All the elements in verticalCuts are distinct.

Analysis

  题目是切蛋糕的问题，题目先给出了蛋糕的size，但是没有给出具体的位置。然后再给出了若干个竖直方向、水平方向的切割线，问能够切除最大块的蛋糕是多大？

  这道题目给出的信息很多，而且不确定的因素很大，蛋糕的位置未知，一开始入手比较困难。我们先不管蛋糕的位置，先看切完之后最大的格子是多大。切的格子要大，肯定是长和宽都要大，所以就需要找到各自方向上，相差最大的两条切割线。这里首先对切线排序，然后找到差最大的两条线，此时两个最大的差的乘积就是最大的格子的面积。

  此时就需要考虑一些边界的条件了，如果上面计算出来最大的格子的面积比蛋糕的水平大，所以初始化的时候需要把这个考虑上。初始化的时候比较两个值，一个是horizontalCuts[0]，这个指的是距离最上方的距离；另一个要考虑的是h - horizontalCuts[size - 1]，这个指的是蛋糕的高度与最后一切的距离差，如果蛋糕的高度比最后一切的高度小，那么蛋糕必然是顶着最上面摆放才能得到最优解。

Solution

  无

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
        sort(horizontalCuts.begin(), horizontalCuts.end());
        sort(verticalCuts.begin(), verticalCuts.end());
        
        int size1 = horizontalCuts.size(), size2 = verticalCuts.size();
        
        int hor_diff = max(horizontalCuts[0], h - horizontalCuts[size1 - 1]), ver_diff = max(verticalCuts[0], w - verticalCuts[size2 - 1]);
        
        for (int i = 1; i < size1; i++) {
            hor_diff = max(hor_diff, horizontalCuts[i] - horizontalCuts[i - 1]);
        }
        for (int i = 1; i < size2; i++) {
            ver_diff = max(ver_diff, verticalCuts[i] - verticalCuts[i - 1]);
        }
        int MOD = 1e9 + 7;
        return (long long)(hor_diff % MOD) * (long long)(ver_diff % MOD) % MOD;
    }
};

Summary

  这道题是比较难的智力题，难度在于初始化条件。这道题目的分享到这里，感谢你的支持！

Welcome to my other publishing channels