Halo

A magic place for coding

0%

LeetCode解题报告（400) -- 587. Erect the Fence

Posted on Valine:

Problem

You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden.

You are asked to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed.

Return the coordinates of trees that are exactly located on the fence perimeter.

Example 1:

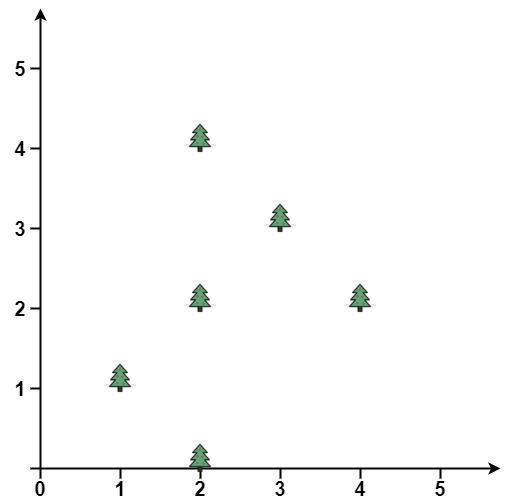
Example1

1
2
Input: points = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [[1,1],[2,0],[3,3],[2,4],[4,2]]

Example 2:

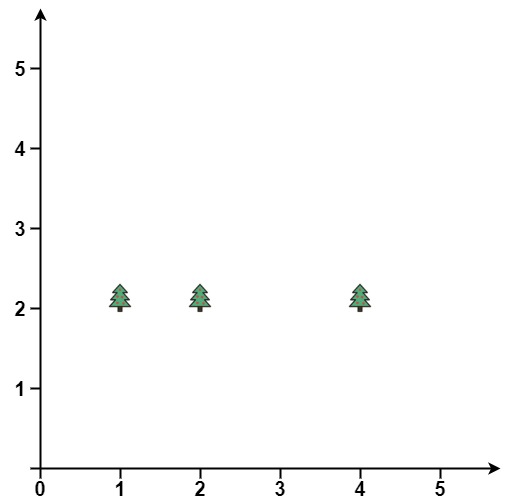
Example2

1
2
Input: points = [[1,2],[2,2],[4,2]]
Output: [[4,2],[2,2],[1,2]]

Constraints:

  • 1 <= points.length <= 3000
  • points[i].length == 2
  • 0 <= xi, yi <= 100
  • All the given points are unique.

Analysis

  又是一道hard，先来读题目。题目给出了若干个坐标点，然后需要我们找出所有的边界点。也就是说，所有的点都需要在这个范围内。涉及到了坐标和点的位置，这道题目有点偏向于计算几何。我们先来看下面的边，图中所有的点都必须要在下面这条边上面；再看上面的边，图中所有的点都必须要在上面这条边的下面，因此我们就可以利用这个特点去进行求解。

  我们先把所有的点按照横坐标排序，如果横坐标相同再按纵坐标排序。排序过后我们从头到尾遍历，也就是在二维平面上从左到右遍历。我们把所有的点都存到一个栈中，之所以用栈，是因为我们要用最新的两个点，和当前的trees[i]（i >= 2）做计算，我们要判断出位于栈顶的点，是否在最外面。这里举个例子，比如倒数第二个点是p，倒数第一个点是q，trees[i]是r，那么我们检查的是q是在p和r的上面还是下面，如果是在上面，则说明q不是边界点，需要从栈中pop out，然后把r加入到栈中；如果是在下面，则说明q是边界点，只需要把r加入到栈中即可。至于怎么判断在上面还是下面后面展开说。

  我们从左到右完成一遍后，就相当于完成了下边界，那么还有上边界呢？道理是一样的，我们只需要从右到左遍历，采用相同的方法去判断出点的位置，然后加入到栈中即可。最后利用set对点进行去重，返回结果即可。

  这里详细分析怎么判断三个点的位置（参考：Orientation of 3 ordered points）。以下边界为例，同样是p、q、r三个点。我们要判断的是q在pr连线的上方还是下方，其实可以转化为计算pq、qr两条直线的斜率：

  1. 如果pq的斜率小于qr的斜率，说明q在pr的下方，此时是不需要pop的；
  2. 如果pq的斜率大于qr的斜率，说明q在pr的上方，此时是需要pop出q。

  转换为计算表达式，假设$P(x_1, y_1)$、$Q(x_2, y_2)$、$R(x_3, y_3)$，计算两者斜率之差为$(y_2 - y_1)(x_3 - x_2) - (y_3 - y_2)(x_2 - x_1)$，如果这个值大于0，说明需要pop；否则保留。

Solution

  无

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
        sort(trees.begin(), trees.end(), [](vector<int> &a, vector<int> &b) {
           if (a[0] == b[0]) {
               return a[1] < b[1];
           } else {
               return a[0] < b[0];
           }
        });
        
        vector<vector<int>> st;
        int size = trees.size();
        for (int i = 0; i < size; i++) {
            while (st.size() >= 2 && orientation(st[st.size() - 2], st[st.size() - 1], trees[i]) > 0) {
                st.pop_back();
            }
            st.push_back(trees[i]);
        }
        st.pop_back();
        for (int i = size - 1; i >= 0; i--) {
            while (st.size() >= 2 && orientation(st[st.size() - 2], st[st.size() - 1], trees[i]) > 0) {
                st.pop_back();
            }
            st.push_back(trees[i]);
        }
        
        set<vector<int>> s(st.begin(), st.end());
        vector<vector<int>> result(s.begin(), s.end());
        return result;
    }
private:
    int orientation(vector<int> p, vector<int> q, vector<int> r) {
        return (q[1] - p[1]) * (r[0] - q[0]) - (r[1] - q[1]) * (q[0] - p[0]);
    }
};

Summary

  这道题目是一道与数学几何相关比较强的题目，里面包含了一些计算集合的知识。思路上比较直观，就是逐个点判断，难点就是判断三个点的相对关系。感谢你的支持！

Welcome to my other publishing channels