LeetCode解题报告（402) -- 834. Sum of Distances in Tree

Problem

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.

Example 1:

Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Example 2:

1 2	Input: n = 1, edges = [] Output: [0]

Example 3:

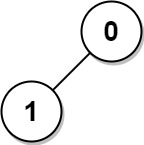
1 2	Input: n = 2, edges = [[1,0]] Output: [1,1]

Constraints:

1 <= n <= 3 * 104
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
The given input represents a valid tree.

Analysis

最近刷hard上瘾了，今天这题依旧是hard。题目以边的形式给出一个无向图，对每个节点，要求计算其他所有的节点到它的距离。一下子没有头绪，那就从例子入手。

当只有一个节点时，答案是0；
当有两个节点时，答案是[1, 1]；
当有三个节点时，比如
1
2
3
0
/ \
1 2
答案是[2, 1, 1]；
当有四个节点时，比如
1
2
3
4
5
0
/ \
1 2
/ \
3 4
以1为根节点的子树和上面三个节点的例子是一样的，以2为根节点的子树和上面一个节点的例子也是一样的，然后我们看以0为根节点的情况。它的值是6，是怎么计算得来的？我们基于它的子树计算，先看左子树（以1为根节点），里面每个节点到0的距离都是每个节点到1的距离+1，同理0到每个节点的距离都是1到每个节点的距离+1，所以这里总的距离增加的量就是左子树的节点数量3个；再看右子树，右子树只有一个以2为根的子树，所以距离是0，有1个节点，因此总的增加距离就是1。

通过分析我们能够得到，每个子树中的节点到子树根节点距离之和等于所有子节点的距离之和加上以子节点为根的子树的节点个数。有点混乱，直接看代码表示。定义count[i]为以i为根节点的子树的节点个数（包括根节点本身），result[i]为以i为根节点其他所有节点到i的距离之和，于是我们有：

count[root] = sum(count[i]) + 1
result[root] = sum(result[i]) + sum(count[i])

其中root是子树根节点，i是与root直接相连的节点

我们可以通过递归求出count和result，但这里的result还不是最终的答案，因为我们定义的是以i为根节点其他所有节点到i的距离之和，还没有考虑子树外的节点到i的距离。但是有一个特殊的值是和最终答案一致的！那就是result[root]，我们就可以借用这个信息去计算其他的result[i]。假设我们计算root的左子树i的result[i]，我们知道，count[root]是root所有子节点的个数，而这count[root]个节点在计算result[root]时，计算的都是到root的距离，现在只要到i的距离，所以是都减少了1；而其他的n - count[root]个节点（不在以root为根的树内）到i的距离都+1，所以就有：

1	result[i] = result[root] - count[i] + n - count[i]

Solution

无

Code

class Solution {
public:
    vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
        vector<vector<int>> tree(n);
        for (auto &edge: edges) {
            tree[edge[0]].push_back(edge[1]);
            tree[edge[1]].push_back(edge[0]);
        }
        
        vector<int> count(n, 0), result(n, 0);
        helper(tree, 0, -1, count, result);
        helper2(tree, 0, -1, count, result);
        return result;
    }
private:
    void helper(vector<vector<int>>& tree, int cur, int pre, vector<int> &count, vector<int> &result) {
        for (int i: tree[cur]) {
            if (i == pre) {
                continue;
            }
            helper(tree, i, cur, count, result);
            count[cur] += count[i];
            result[cur] += result[i] + count[i];
        }
        count[cur]++;
    }
    
    void helper2(vector<vector<int>>& tree, int cur, int pre, vector<int> &count, vector<int> &result) {
        for (int i: tree[cur]) {
            if (i == pre) {
                continue;
            }
            result[i] = result[cur] - count[i] + result.size() - count[i];
            helper2(tree, i, cur, count, result);
        }
    }
};

Summary

这道题目是一道非常综合的题目，先是要求构建图，然后是利用递归进行遍历，同时还要找到长度和节点数量的大小关系。这道题目的分享到这里，感谢你的支持！