LeetCode解题报告（405) -- 764. Largest Plus Sign

Problem

You are given an integer n. You have an n x n binary grid grid with all values initially 1‘s except for some indices given in the array mines. The ith element of the array mines is defined as mines[i] = [xi, yi] where grid[xi][yi] == 0.

Return the order of the largest axis-aligned plus sign of 1*’s contained in* grid. If there is none, return 0.

An axis-aligned plus sign of 1‘s of order k has some center grid[r][c] == 1 along with four arms of length k - 1 going up, down, left, and right, and made of 1‘s. Note that there could be 0‘s or 1‘s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for 1‘s.

Example 1:

1
2
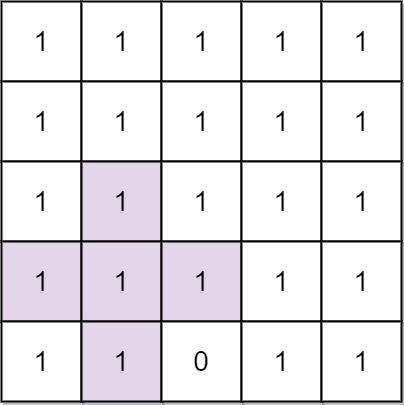
3

Input: n = 5, mines = [[4,2]]
Output: 2
Explanation: In the above grid, the largest plus sign can only be of order 2. One of them is shown.

Example 2:

1
2
3

Input: n = 1, mines = [[0,0]]
Output: 0
Explanation: There is no plus sign, so return 0.

Constraints:

1 <= n <= 500
1 <= mines.length <= 5000
0 <= xi, yi < n
All the pairs (xi, yi) are unique.

Analysis

题目给出矩阵的边长，同时还有里面为0的位置，其余位置都是1。问最大的由1组成的十字有多大？这个值是由四个方向的长度的最小值决定的，所以我们需要对四个方向都计算一边，然后求一个最小值。这是最暴力的解法，当然是过不了OJ的，但是思路基本是这样。

上面暴力的解法最重要的问题是他有大量的重复计算，解决重复计算的方法最好就是用dp。因此我们建立一个二维的dp矩阵，从四个方向都dp一遍，记录每个位置上、下、左、右四个方向最长的长度。因为这里我们要求四个方向的最小值，所以并不需要四个方向各开一个dp，共用1个取最小值就可以了。

Solution

无

Code

class Solution {
public:
    int orderOfLargestPlusSign(int n, vector<vector<int>>& mines) {
        vector<vector<int>> matrix(n, vector<int>(n, 0));
        
        set<int> s;
        for (auto &mine: mines) {
            s.insert(mine[0] * n + mine[1]);
        }
        
        int cnt = 0;
        for (int i = 0; i < n; i++) {
            cnt = 0;
            for (int j = 0; j < n; j++) {
                cnt = s.count(i * n + j)? 0: cnt + 1;
                matrix[i][j] = cnt;
            }
            cnt = 0;
            for (int j = n - 1; j >= 0; j--) {
                cnt = s.count(i * n + j)? 0: cnt + 1;
                matrix[i][j] = min(matrix[i][j], cnt);
            }
        }
        
        int result = 0;
        for (int j = 0; j < n; j++) {
            cnt = 0;
            for (int i = 0; i < n; i++) {
                cnt = s.count(i * n + j)? 0: cnt + 1;
                matrix[i][j] = min(matrix[i][j], cnt);
            }
            cnt = 0;
            for (int i = n - 1; i >= 0; i--) {
                cnt = s.count(i * n + j)? 0: cnt + 1;
                matrix[i][j] = min(matrix[i][j], cnt);
                result = max(result, matrix[i][j]);
            }
        }
        
        return result;
    }
};

Summary

这道题目基本思路还是二维dp，虽然题目表达上并没有很明确dp的意思，但是仔细分析过后，发现其本质就是dp，dp的转移非常简单。这道题目的分享到这里，感谢你的支持！