LeetCode解题报告（425）-- 1878. Get Biggest Three Rhombus Sums in a Grid

Problem

You are given an m x n integer matrix grid.

A rhombus sum is the sum of the elements that form the border of a regular rhombus shape in grid. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each rhombus sum:

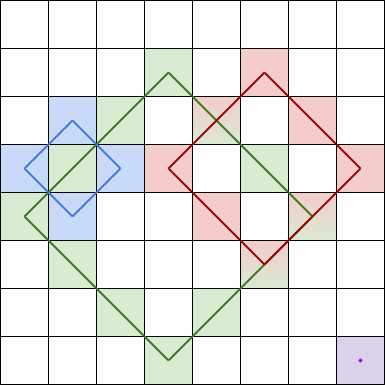
Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.

Return the biggest three distinct rhombus sums in the grid in descending order**. If there are less than three distinct values, return all of them.

Example 1:

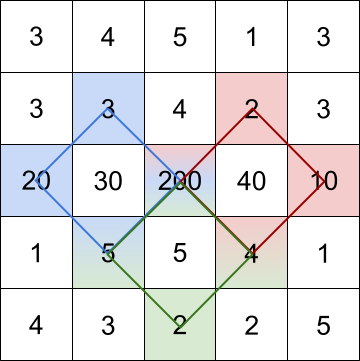
Input: grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
Output: [228,216,211]
Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 20 + 3 + 200 + 5 = 228
- Red: 200 + 2 + 10 + 4 = 216
- Green: 5 + 200 + 4 + 2 = 211

Example 2:

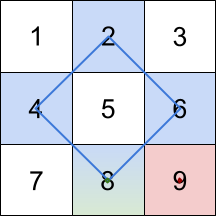
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: [20,9,8]
Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 4 + 2 + 6 + 8 = 20
- Red: 9 (area 0 rhombus in the bottom right corner)
- Green: 8 (area 0 rhombus in the bottom middle)

Example 3:

1
2
3

Input: grid = [[7,7,7]]
Output: [7]
Explanation: All three possible rhombus sums are the same, so return [7].

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 105

Analysis

题目给出一个矩阵，这次要求的是菱形的sum，菱形的sum定义为它边经过的位置的数字之和。hint中已经告诉我们可以采用暴力的手段来进行求解，但这里我们还是想做的相对比较好。我们想回想一下，对于正方形求和，我们会怎么做？

毫无疑问答案应该是前缀和，我们可以首先计算出前缀和，然后在计算时就能快速计算某条边的和。那我们这里能不能用同样的思路呢？当然是可以的。菱形有四条边，/这个方向有两条，\这个方向也有两条，所以我们要预先求出/方向和\方向的前缀和。计算公式为：
$$
sum1[i][j] = sum1[i - 1][j - 1] + grid[i - 1][j - 1] \
sum2[i][j] = sum2[i - 1][j + 1] + grid[i - 1][j - 1]
$$
有了这个前缀和，我们先来看怎么使用。对于/这个方向，如果我的左下方的起点为(lx, ly)，右上方的终点为(ux, uy)，那么前缀和为sum1[lx + 1][ly + 1] - sum1[ux][uy + 2]。这里探讨一下为什么是sum1[ux][uy + 2]，原因是以右上方的终点作为起点的前缀和是sum1[ux + 1][uy + 1]，因为我们的计算需要包含这个点，所以要减去他右上方的点，因此要减去sum1[ux][uy + 2]。

计算出前缀和并知道怎么使用了，接下来就是遍历所有的菱形，确定一个菱形也不难，以每个位置作为菱形的上顶点，然后遍历所有的宽度k，分别计算出左、右、下顶点，然后计算出前缀和。这里还需要减去四个顶点的值，因为计算前缀和的时候重复计算了。

这道题目还有一个难点是要求返回前三大的值，而且还要是distinct。如果使用priority queue确实可以维护前三大，但是唯一性就有点麻烦，所以这里我直接使用set，它自带排序功能，从小到大。

Solution

无。

Code

class Solution {
public:
    vector<int> getBiggestThree(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        
        vector<vector<int>> sum1(m + 1, vector<int>(n + 2));
        vector<vector<int>> sum2(m + 1, vector<int>(n + 2));
        
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                sum1[i][j] = sum1[i - 1][j - 1] + grid[i - 1][j - 1];
                sum2[i][j] = sum2[i - 1][j + 1] + grid[i - 1][j - 1];
            }
        }
        set<int> pq;
        
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                pq.insert(grid[i][j]); // single grid is also valid
                if (pq.size() > 3) {
                    pq.erase(pq.begin());
                }
                for (int k = i + 2; k < m; k += 2) {
                    int ux = i, uy = j;
                    int dx = k, dy = j;
                    
                    int lx = (i + k) / 2, ly = j - (k - i) / 2;
                    int rx = (i + k) / 2, ry = j +  (k - i) / 2;
                    
                    if (ly < 0 || ry >= n) {
                        break;
                    }
                    int sum = (sum2[lx + 1][ly + 1] - sum2[ux][uy + 2]) + (sum1[rx + 1][ry + 1] - sum1[ux][uy]) + (sum1[dx + 1][dy + 1] - sum1[lx][ly]) + (sum2[dx + 1][dy + 1] - sum2[rx][ry + 2]) - (grid[ux][uy] + grid[lx][ly] + grid[rx][ry] + grid[dx][dy]);
                    pq.insert(sum);
                    //cout << sum << endl;
                    if (pq.size() > 3) {
                        pq.erase(pq.begin());
                    }
                }
            }
        }
        
        vector<int> result(pq.size());
        int idx = pq.size() - 1;
        for (auto num: pq) {
            result[idx--] = num;
        }
        return result;
    }
};

Summary

这道题目是一道比较综合的题目，包括了前缀和的使用、矩阵遍历、前k大唯一值这几个知识点，虽然这几个点都是非常常见的，但是转移到菱形这个背景下就变得有点难了。这道题目尤其需要深刻理解前缀和的意义及使用方式。这道题目的分享到这里，感谢你的支持！