LeetCode解题报告（463）-- 2039. The Time When the Network Becomes Idle

Problem

There is a network of n servers, labeled from 0 to n - 1. You are given a 2D integer array edges, where edges[i] = [ui, vi] indicates there is a message channel between servers ui and vi, and they can pass any number of messages to each other directly in one second. You are also given a 0-indexed integer array patience of length n.

All servers are connected, i.e., a message can be passed from one server to any other server(s) directly or indirectly through the message channels.

The server labeled 0 is the master server. The rest are data servers. Each data server needs to send its message to the master server for processing and wait for a reply. Messages move between servers optimally, so every message takes the least amount of time to arrive at the master server. The master server will process all newly arrived messages instantly and send a reply to the originating server via the reversed path the message had gone through.

At the beginning of second 0, each data server sends its message to be processed. Starting from second 1, at the beginning of every second, each data server will check if it has received a reply to the message it sent (including any newly arrived replies) from the master server:

If it has not, it will resend the message periodically. The data server i will resend the message every patience[i] second(s), i.e., the data server i will resend the message if patience[i] second(s) have elapsed since the last time the message was sent from this server.
Otherwise, no more resending will occur from this server.

The network becomes idle when there are no messages passing between servers or arriving at servers.

Return the earliest second starting from which the network becomes idle.

Example 1:

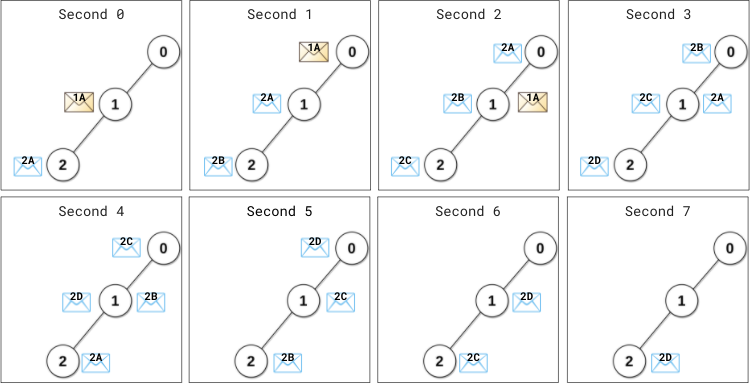
Input: edges = [[0,1],[1,2]], patience = [0,2,1]
Output: 8
Explanation:
At (the beginning of) second 0,
- Data server 1 sends its message (denoted 1A) to the master server.
- Data server 2 sends its message (denoted 2A) to the master server.

At second 1,
- Message 1A arrives at the master server. Master server processes message 1A instantly and sends a reply 1A back.
- Server 1 has not received any reply. 1 second (1 < patience[1] = 2) elapsed since this server has sent the message, therefore it does not resend the message.
- Server 2 has not received any reply. 1 second (1 == patience[2] = 1) elapsed since this server has sent the message, therefore it resends the message (denoted 2B).

At second 2,
- The reply 1A arrives at server 1. No more resending will occur from server 1.
- Message 2A arrives at the master server. Master server processes message 2A instantly and sends a reply 2A back.
- Server 2 resends the message (denoted 2C).
...
At second 4,
- The reply 2A arrives at server 2. No more resending will occur from server 2.
...
At second 7, reply 2D arrives at server 2.

Starting from the beginning of the second 8, there are no messages passing between servers or arriving at servers.
This is the time when the network becomes idle.

Example 2:

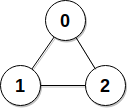
Input: edges = [[0,1],[0,2],[1,2]], patience = [0,10,10]
Output: 3
Explanation: Data servers 1 and 2 receive a reply back at the beginning of second 2.
From the beginning of the second 3, the network becomes idle.

Constraints:

n == patience.length
2 <= n <= 105
patience[0] == 0
1 <= patience[i] <= 105 for 1 <= i < n
1 <= edges.length <= min(105, n * (n - 1) / 2)
edges[i].length == 2
0 <= ui, vi < n
ui != vi
There are no duplicate edges.
Each server can directly or indirectly reach another server.

Analysis

题目给出一个图，其中0表示master server，其他的表示data server。data server会向master发消息，master收到后发送确认给data server，两者的沟通走的都是最短路径。然后还有一个patience[i]，表明server[i]多久没收到确认消息就会重发一次。题目问经过多久后，整个网络将会没有消息发送。

首先我们理一下整个工作过程：

首先找到每个data server到master的最短路径；
然后一开始所有的data server都向master发出消息；
有一段时间data server还没收到master返回的确认消息，而又已经到了patience[i]，所以需要重发；
data server收到了第一次发送的消息的确认，此时开始data server将不再进行重发。这里有人会问，会不会又超过了patience[i]呢？答案是不会的，因为重发的间隔就是patience[i]。
后面一直都能收到确认，直到最后一个消息的确认返回。

这道题目是没有冲突的，也就是不同的消息传输过程中不会相互影响，所以我们可以单独考虑每一个data server，每一个data server都计算出什么时候become idle，最后取一个最大值就可以了。

按照上面的步骤，先用BFS从master节点开始找每个data server的最短路径，用一个数组time记录下来。然后我们要计算出重发了多少条消息，如果路径长度为n，那么第一条消息的确认回到data server的时间就是2n，所以前一秒就是2n - 1。然后发送的频率是patience[i]，所以重发消息的数量就是(2n - 1) / patience[i]。那么最后一条重发是什么时候呢？先说为什么要算这个时间，因为上面第5步说了，当最后一条重发完之后，后面就不再会有重发了，只需要等最后一条消息走完整个过程就可以。最后一条重发的时间就是2n - 1，然后加上最后一条消息走完的时间，因此最后忙碌的时间就是(2n - 1) + 2n。

对每个data server都处理一边维护最大值，还要注意，这个时间是data server收到最后一条消息确认的时间，因为题目要求的是idle，因此要+1。

Solution

无。

Code

class Solution {
public:
    int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& patience) {
        int size = patience.size();
        vector<vector<int>> graph(size);
        
        for (vector<int> &edge: edges) {
            graph[edge[0]].push_back(edge[1]);
            graph[edge[1]].push_back(edge[0]);
        }
        
        vector<int> time(size, -1);
        time[0] = 0;
        queue<int> q;
        q.push(0);
        
        while (!q.empty()) {
            int s = q.size();
            for (int i = 0; i < s; ++i) {
                int cur = q.front();
                q.pop();
                
                for (int next: graph[cur]) {
                    if (time[next] == -1) {
                        time[next] = time[cur] + 1;
                        q.push(next);
                    }
                }
            }
        }
        
        int result = 0;
        for (int i = 1; i < size; ++i) {
            int extra = (time[i] * 2 - 1) / patience[i];
            int lastOut = extra * patience[i];
            int lastIn = lastOut + time[i] * 2;
            
            result = max(result, lastIn);
        }
        return result + 1;
    }
};

Summary

这道题目考察了BFS，这个是比较简单的，难点在于分析出整个重发的过程，以最后一次重发消息为分界点，去进行计算。这道题目的分享到这里，感谢你的支持！