LeetCode解题报告（468）-- 1080. Insufficient Nodes in Root to Leaf Paths

Problem

Given the root of a binary tree and an integer limit, delete all insufficient nodes in the tree simultaneously, and return the root of the resulting binary tree.

A node is insufficient if every root to leaf path intersecting this node has a sum strictly less than limit.

A leaf is a node with no children.

Example 1:

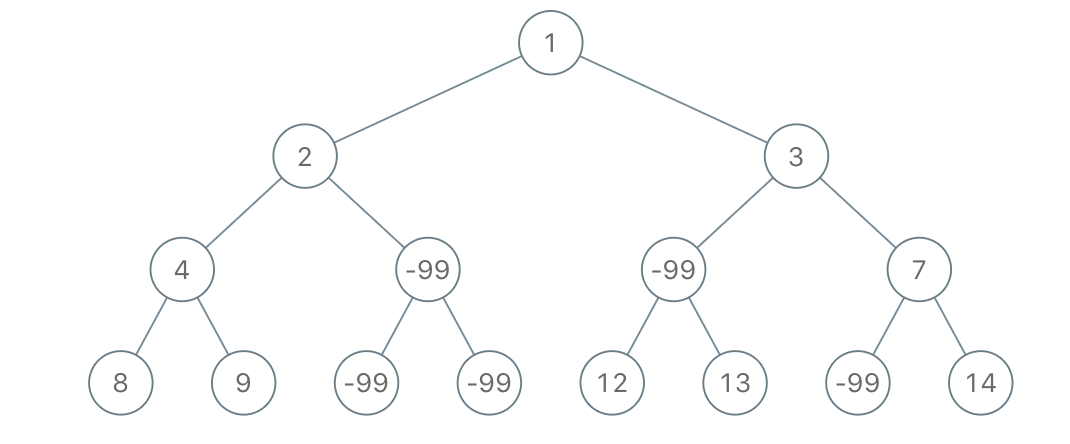
1 2	Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1 Output: [1,2,3,4,null,null,7,8,9,null,14]

Example 2:

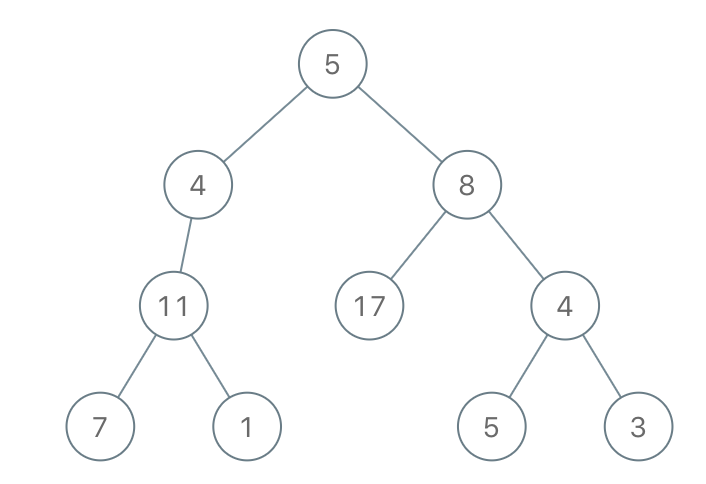
1 2	Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22 Output: [5,4,8,11,null,17,4,7,null,null,null,5]

Example 3:

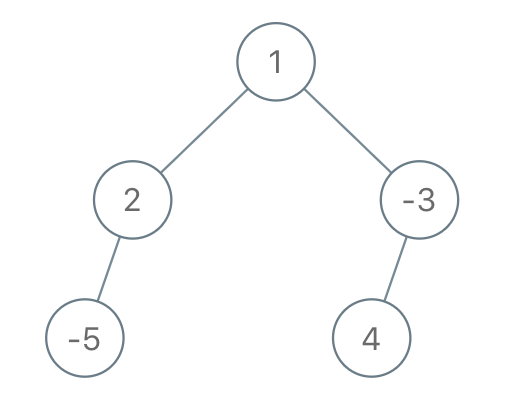
1 2	Input: root = [1,2,-3,-5,null,4,null], limit = -1 Output: [1,null,-3,4]

Constraints:

The number of nodes in the tree is in the range [1, 5000].
-105 <= Node.val <= 105
-109 <= limit <= 109

Analysis

题目给出一颗二叉树，要求删除这颗树上所有的insufficient nodes。定义insufficient node为所有经过该节点的从根节点到叶子节点的路径的和严格小于limit。对于二叉树的题目我们还是优先考虑递归解法，我们先来看节点有几种情况：

如果节点是叶子节点：我们判断sum是否小于limit，其实如果通过递归解法的话，我们每经过一个节点，就可以limit - node->val，继续传给子节点，当叶子节点的node->val < limit时，说明当前这个节点就要被删除了，因为经过当前节点的，从根节点到叶子节点的路径只有一条。
如果节点不是叶子节点，它并不需要判断和limit的关系，而是递归调用时传入limit - node->val，当递归完左右子树，发现都变成nullptr，也就是说经过这个节点的两条路径（所有路径）的和都小于limit，所以它的叶子节点才被删掉，这个节点也应该被删掉。

经过上面的分析，我们知道了如何判断怎么删除，递归时删除我之前说过，直接return nullptr就是删除。

Solution

无。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        if (!root) {
            return nullptr;
        }
        
        if (!root->left && !root->right) {
            return (root->val < limit ? nullptr: root);
        }
        
        root->left = sufficientSubset(root->left, limit - root->val);
        root->right = sufficientSubset(root->right, limit - root->val);
        if (!root->left && !root->right) {
            return nullptr;
        }
        return root;
    }
};

Summary

这道题目是二叉树中比较正常的题目，也是通过路径和去做一些逻辑判断，这里就是删除。这道题目的分享到这里，感谢你的支持！