Problem
Given an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.
A full binary tree is a binary tree where each node has exactly 0 or 2 children.
Example 1:
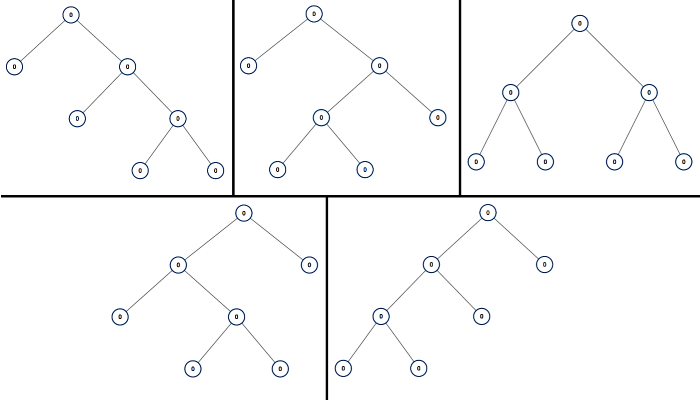
1 | Input: n = 7 |
Example 2:
1 | Input: n = 3 |
Constraints:
1 <= n <= 20
Analysis
题目给出一个数字n,要求返回所有形态的满二叉树。这种要返回全部结果的题目,一般都是穷举加上记忆化数组。首先题目说了二叉树中节点的值都是0,所以我们不用考虑节点的值,只考虑形态。同时题目限定了是满二叉树,满二叉树的节点数量肯定是奇数,所以可以跳过偶数的情况。
先看base case,base case就是只有一个节点,返回自己即可。然后看general的case,我们把二叉树分成左右两部分,因此需要把两边的情况都组合一边放入到答案中。注意到这里有很多的重复计算,所以我们可以用一个unordered_map把计算结果缓存起来,加速运算。
Solution
无。
Code
1 | /** |
Summary
这道题目是比较简单的记忆化搜索,需要注意的点也不多。这道题目的分享到这里,感谢你的支持!

