LeetCode解题报告（480）-- 1039. Minimum Score Triangulation of Polygon

Problem

You have a convex n-sided polygon where each vertex has an integer value. You are given an integer array values where values[i] is the value of the ith vertex (i.e., clockwise order).

You will triangulate the polygon into n - 2 triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all n - 2 triangles in the triangulation.

Return the smallest possible total score that you can achieve with some triangulation of the polygon.

Example 1:

1
2
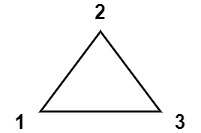
3

Input: values = [1,2,3]
Output: 6
Explanation: The polygon is already triangulated, and the score of the only triangle is 6.

Example 2:

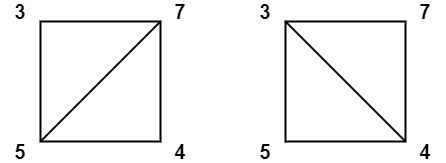
Input: values = [3,7,4,5]
Output: 144
Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144.
The minimum score is 144.

Example 3:

1
2
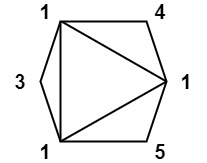
3

Input: values = [1,3,1,4,1,5]
Output: 13
Explanation: The minimum score triangulation has score 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.

Constraints:

n == values.length
3 <= n <= 50
1 <= values[i] <= 100

Analysis

题目的背景是一个多边形，多边形上的每个顶点都有一个值，我们通过把多边形划分成多个三角形，然后计算出划分的score。划分的score为每个三角形三个顶点的乘积之和。首先第一反应就是划分的情况有很多，第二个就是最后要求的是一个极值，所以这两个特点都指向了dp，或者说是记忆化搜索。那么问题就变成了按照什么顺序去搜索比较有条理呢？

题目计算的是三角形，我们可以从这个入手，也就是说如果确定了两个顶点，也就确定了一条边，然后我们通过更改第三个顶点去构造出不同的三角形，这个好处是避免了在多边形内，不同三角形相互交错了。于是我们直接定义dp[i][j]为以(i, j)为边，第三个的范围在[i + 1, j)的最小score。如果我们从dp[0][n - 1]开始计算，那么第三个点的范围就一定在[i + 1, j)（保证了大小关系），因此我们就可以用top-down dp的方法进行计算。

Solution

无。

Code

class Solution {
public:
    int minScoreTriangulation(vector<int>& values) {
        int n = values.size();
        vector<vector<int>> dp(n, vector<int>(n, -1));
        return helper(values, 0, n - 1, dp);
    }
private:
    int helper(vector<int>& values, int i, int j, vector<vector<int>>& dp) {
        if (i >= j - 1) {
            return 0;
        }
        if (dp[i][j] != -1) {
            return dp[i][j];
        }
        int result = INT_MAX;
        for (int k = i + 1; k < j; ++k) {
            result = min(result, helper(values, i, k, dp) + helper(values, k, j, dp) + values[i] * values[j] * values[k]);
        }
        //cout << result << endl;
        return dp[i][j] = result;
    }
};

Summary

这道题目是比较经典的top down dp做法，难点在于如何按照一定的顺序切分三角形并计算顶点值。这道题目的分享到这里，感谢你的支持！