LeetCode解题报告（482）-- 662. Maximum Width of Binary Tree

Problem

Given the root of a binary tree, return the maximum width of the given tree.

The maximum width of a tree is the maximum width among all levels.

The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes are also counted into the length calculation.

It is guaranteed that the answer will in the range of 32-bit signed integer.

Example 1:

1
2
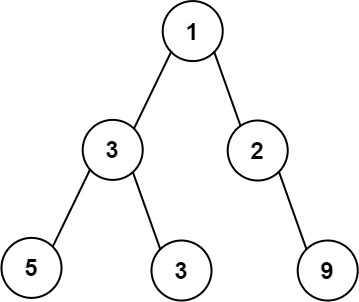
3

Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).

Example 2:

1
2
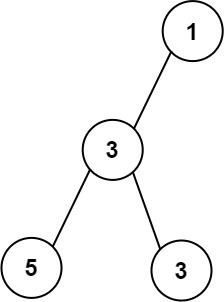
3

Input: root = [1,3,null,5,3]
Output: 2
Explanation: The maximum width existing in the third level with the length 2 (5,3).

Example 3:

1
2
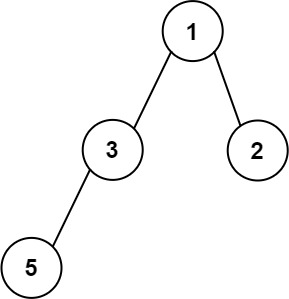
3

Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width existing in the second level with the length 2 (3,2).

Constraints:

The number of nodes in the tree is in the range [1, 3000].
-100 <= Node.val <= 100

Analysis

题目意思很简单，给出一颗二叉树，要求求出树的宽度。首先这里要明确什么是宽度，我一开始的做法是BFS，根节点的坐标为0，左节点-1，右节点+1，但是这样算出来的并不是最大宽度，因为它只计算了相对于根节点的位置，并不能计算出坐标重复的情况，所以更好的做法应该是采用满二叉树的下标计算方法，即假设根节点的下标为i，其左子节点的下标为2 * i，右子节点的下标为2 * i + 1，BFS时只需要把每层最右的下标减去最左的下标+1就是该层的宽度。

Solution

这道题目还有一个越界的坑，当我们使用满二叉树下标计算方法，当树的层数很深时，就算节点很少，也会造成int越界，这里的解决方法也很巧妙，因为层与层的计算是独立的，而且我们只关心一个差值，至于这个下标实际是多少我们并不care，所以每层计算完之后，我们都做一个归零处理。

比如第i层的第一个节点下标是x，那么处理这层所有的下标减去x，这样就能防止下标越界了。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        if (!root) {
            return 0;
        }
        
        long result = 1;
        queue<pair<TreeNode*, long>> q;
        q.push({root, 1});
        
        while (!q.empty()) {
            int size = q.size();
            if (size == 1) {
                q.front().second = 1;
            }
            int mmin = q.front().second;
            
            result = max(result, q.back().second - q.front().second + 1);
            
            for (int i = 0; i < size; ++i) {
                auto cur = q.front();
                q.pop();
                auto idx = cur.second - mmin;                
                if (cur.first->left) {
                    q.push({cur.first->left, 2 * idx});
                }
                
                if (cur.first->right) {
                    q.push({cur.first->right, 2 * idx + 1});
                }
            }
            
        }
        return result;
    }
};

Summary

这道题目是二叉树中一道比较有意思的题目，其中对于越界情况的处理比较值得总结。这道题目的分享到这里，感谢你的支持！