LeetCode解题报告（486）-- 305. Number of Islands II

Problem

You are given an empty 2D binary grid grid of size m x n. The grid represents a map where 0‘s represent water and 1‘s represent land. Initially, all the cells of grid are water cells (i.e., all the cells are 0‘s).

We may perform an add land operation which turns the water at position into a land. You are given an array positions where positions[i] = [ri, ci] is the position (ri, ci) at which we should operate the ith operation.

Return an array of integers answer where answer[i] is the number of islands after turning the cell (ri, ci) into a land.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

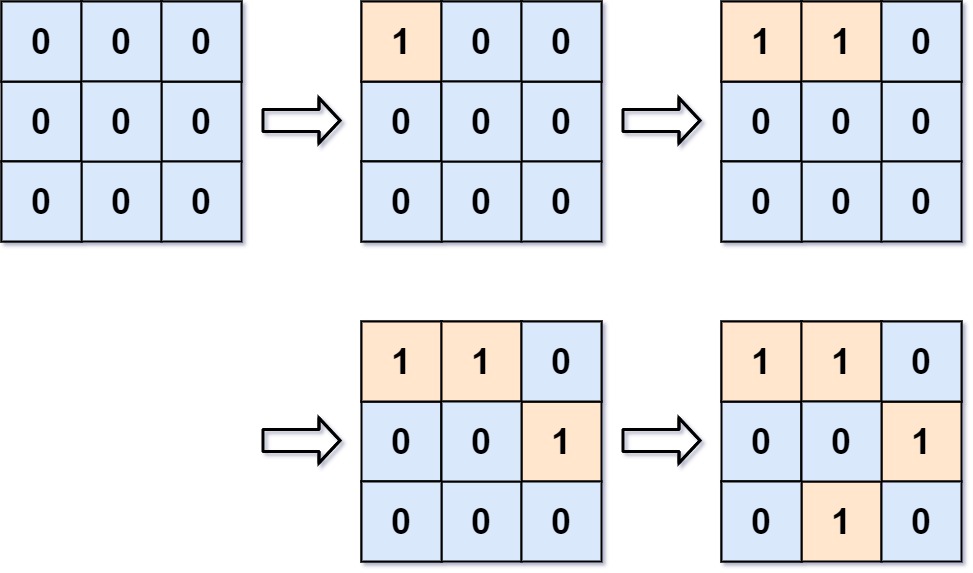
Example 1:

Input: m = 3, n = 3, positions = [[0,0],[0,1],[1,2],[2,1]]
Output: [1,1,2,3]
Explanation:
Initially, the 2d grid is filled with water.
- Operation #1: addLand(0, 0) turns the water at grid[0][0] into a land. We have 1 island.
- Operation #2: addLand(0, 1) turns the water at grid[0][1] into a land. We still have 1 island.
- Operation #3: addLand(1, 2) turns the water at grid[1][2] into a land. We have 2 islands.
- Operation #4: addLand(2, 1) turns the water at grid[2][1] into a land. We have 3 islands.

Example 2:

1 2	Input: m = 1, n = 1, positions = [[0,0]] Output: [1]

Constraints:

1 <= m, n, positions.length <= 104
1 <= m * n <= 104
positions[i].length == 2
0 <= ri < m
0 <= ci < n

Follow up: Could you solve it in time complexity O(k log(mn)), where k == positions.length?

Analysis

这是Number of Islands的系列题，之前的题目就是简单的BFS/DFS。这道题目稍微有点不同，题目给出一个positions数组，里面每个position = [i, j]，表明把[i, j]这个位置从水变为陆地，问每一步之后图中一共有多少个陆地。这是一道非常明显的动态维护连通性的问题，动态维护这个特点直接考虑用并查集做。并查集的实现不在这里赘述，我们遍历positions，对于每一个位置，先把其本身变为陆地，然后遍历其四个方向的邻居检查一下能否构成岛屿，如果能够构成岛屿则连接在一起，维护一个连通分量个数。

Solution

这道题目实现上有一些细节需要注意。第一，在并查集的实现中，初始化的时候并不需要把parent[i] = i，因为并不是每个位置都是一个节点，只有是陆地的位置才是一个节点；第二，每次遍历到一个位置后，首先要检查它是否已经是陆地了，如果不是的话设置parent[x] = x，否则直接使用当前的连通分量数量作为答案；第三，为了方便并查集的使用，所有位置都换算成一维坐标访问。

Code

class Solution {
public:
    vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {
        int size = l.size();
        vector<bool> result(size, false);
        
        for (int i = 0; i < size; ++i) {
            int left = l[i], right = r[i], len = right - left + 1;
            int mx = INT_MIN, mi = INT_MAX;
            for (int j = left; j <= right; ++j) {
                mx = max(mx, nums[j]);
                mi = min(mi, nums[j]);
            }
            
            if (mx == mi) {
                result[i] = true;
                continue;
            }
            
            if ((mx - mi) % (len - 1)) {
                continue;
            }
            vector<bool> diffs(len, false);
            int diff = (mx - mi) / (len - 1);
            int j = left;
            for (; j <= right; ++j) {
                if ((nums[j] - mi) % diff || diffs[(nums[j] - mi) / diff]) {
                    break;
                }
                diffs[(nums[j] - mi) / diff] = true;
            }
            
            if (j > right) {
                result[i] = true;
            }
        }
        return result;
    }
};

Summary

这道题目就是很典型的并查集使用，提示也很明显。在二维矩阵中使用并查集要注意下标转换，同时还要特别注意初始化的时机。这道题目的分享到这里，感谢你的支持！