LeetCode解题报告（489）-- 1026. Maximum Difference Between Node and Ancestor

Problem

Given the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val - b.val| and a is an ancestor of b.

A node a is an ancestor of b if either: any child of a is equal to b or any child of a is an ancestor of b.

Example 1:

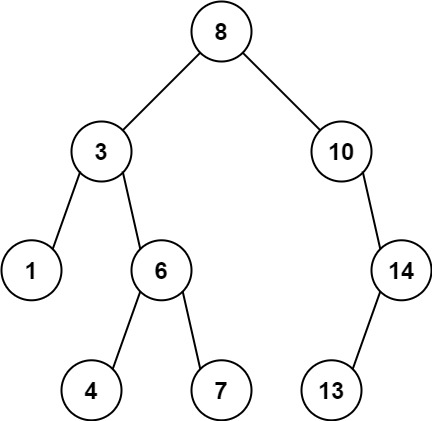
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Example 2:

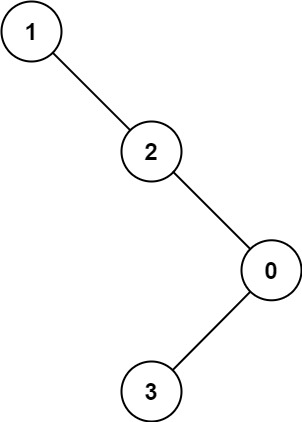
1 2	Input: root = [1,null,2,null,0,3] Output: 3

Constraints:

The number of nodes in the tree is in the range [2, 5000].
0 <= Node.val <= 105

Analysis

题目给出一颗二叉树，要求返回某个节点和祖先节点之间最大的差的绝对值。实际上这个要求就是规定两个节点要在同一条从根到叶子节点的路径上，那么我们做一次先序遍历就好了，维护路径上最大和最小的值，当路径走完的时候，求一下差的绝对值就可以了。递归函数向上返回左子树和右子树较大的绝对值作为答案即可。

Solution

无。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxAncestorDiff(TreeNode* root) {
        if (!root) {
            return 0;
        }
        return helper(root, root->val, root->val);
    }
private:
    int helper(TreeNode* root, int minValue, int maxValue) {
        if (!root) {
            return maxValue - minValue;
        }
        
        maxValue = max(maxValue, root->val);
        minValue = min(minValue, root->val);
        
        int left = helper(root->left, minValue, maxValue);
        int right = helper(root->right, minValue, maxValue);
        
        return max(left, right);
    }
};

Summary

这道题目是比较常规的使用先序遍历求解二叉树的题目，难度在于如何把题目中节点和祖先的关系，转化为在根节点到叶子节点的路径上处理。这道题目的分享到这里，感谢你的支持！