LeetCode解题报告（502）-- 756. Pyramid Transition Matrix

Problem

You are stacking blocks to form a pyramid. Each block has a color, which is represented by a single letter. Each row of blocks contains one less block than the row beneath it and is centered on top.

To make the pyramid aesthetically pleasing, there are only specific triangular patterns that are allowed. A triangular pattern consists of a single block stacked on top of two blocks. The patterns are given as a list of three-letter strings allowed, where the first two characters of a pattern represent the left and right bottom blocks respectively, and the third character is the top block.

For example, "ABC" represents a triangular pattern with a 'C' block stacked on top of an 'A' (left) and 'B' (right) block. Note that this is different from "BAC" where 'B' is on the left bottom and 'A' is on the right bottom.

You start with a bottom row of blocks bottom, given as a single string, that you must use as the base of the pyramid.

Given bottom and allowed, return true if you can build the pyramid all the way to the top such that every triangular pattern in the pyramid is in allowed, or false otherwise.

Example 1:

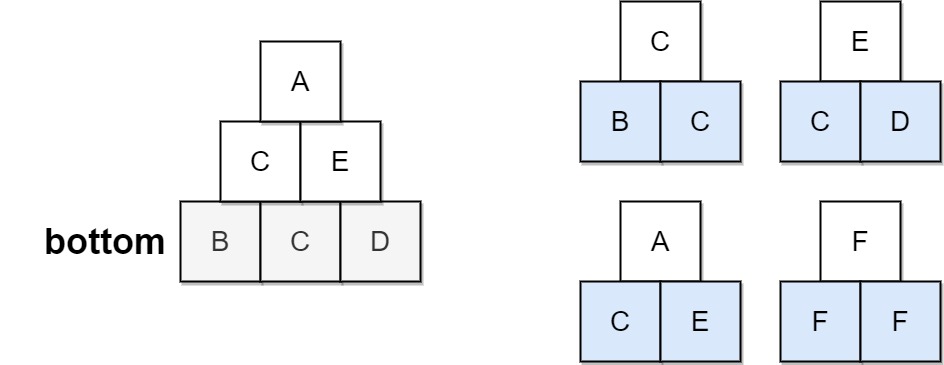
Input: bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"]
Output: true
Explanation: The allowed triangular patterns are shown on the right.
Starting from the bottom (level 3), we can build "CE" on level 2 and then build "E" on level 1.
There are three triangular patterns in the pyramid, which are "BCC", "CDE", and "CEA". All are allowed.

Example 2:

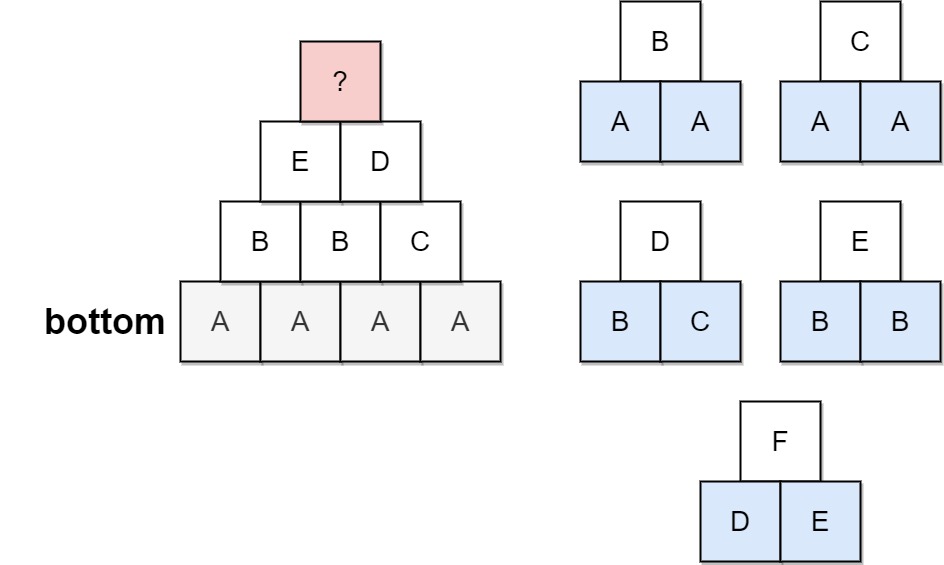
Input: bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"]
Output: false
Explanation: The allowed triangular patterns are shown on the right.
Starting from the bottom (level 4), there are multiple ways to build level 3, but trying all the possibilites, you will get always stuck before building level 1.

Constraints:

2 <= bottom.length <= 6
0 <= allowed.length <= 216
allowed[i].length == 3
The letters in all input strings are from the set {'A', 'B', 'C', 'D', 'E', 'F'}.
All the values of allowed are unique.

Analysis

这道题目给出了一个bottom字符串，还有一个allowed的字符串数组，其中每个字符串的长度都是3，意思是以前两个字符作为base，可以在上面加上第三个字符。所以这实际上就是一个长度为2的字符串到一个字符的映射，我们首先用unordered_map把这种映射记录下来，方便查询。然后我们来看怎么去构建。

因为都是两个字符映射到一个字符，所以我们可以每两个字符串去遍历，然后把所有可能的第三个字符的结果都查找一边，这就有点像DFS了。因为这里实际上是有两层字符串，一层是bottom作为底，另一层是在bottom上面生成的above，我们一直递归下去，如果最后bottom只有一个字符，说明已经构建了一个金字塔，返回true。当没有办法找到下一个字符就返回false。

DFS的套路基本有了，但是还有一个优化的点，需要加上记忆数组，因为我们可能处理很多相同的bottom，所以我们可以把结果存储下来，加快计算。

Solution

无。

Code

class Solution {
public:
    bool pyramidTransition(string bottom, vector<string>& allowed) {
        for (string &str: allowed) {
            st[str.substr(0, 2)].insert(str[2]);
        }
        return helper(bottom, "");
    }
private:
    unordered_map<string, unordered_set<char>> st;
    unordered_map<string, bool> memo;
    bool helper(string current, string above) {
        if (memo.count(current)) {
            return memo[current];
        }
        if (above.size() == current.size() - 1) {
            if (above.empty()) {
                return memo[current] = true;
            }
            else {
                return memo[above] = helper(above, "");
            }
        }
        
        int pos = above.size();
        string base = current.substr(pos, 2);
        
        if (st.count(base)) {
            for (char ch: st[base]) {
                bool ret = helper(current, above + ch);
                if (ret) {
                    return memo[current] = true;
                }
            }
        }
        return false;
    }
};

Summary

这道题目是一个记忆化搜索，首先通过数组构建出映射关系的map，然后对bottom字符串逐个（每两个）遍历，DFS找到下一个状态。最后在运算过程中加上记忆化数组提高搜索效率。这道题目的分享到这里，感谢你的支持！