LeetCode解题报告（511）-- 749. Contain Virus

Problem

A virus is spreading rapidly, and your task is to quarantine the infected area by installing walls.

The world is modeled as an m x n binary grid isInfected, where isInfected[i][j] == 0 represents uninfected cells, and isInfected[i][j] == 1 represents cells contaminated with the virus. A wall (and only one wall) can be installed between any two 4-directionally adjacent cells, on the shared boundary.

Every night, the virus spreads to all neighboring cells in all four directions unless blocked by a wall. Resources are limited. Each day, you can install walls around only one region (i.e., the affected area (continuous block of infected cells) that threatens the most uninfected cells the following night). There will never be a tie.

Return the number of walls used to quarantine all the infected regions. If the world will become fully infected, return the number of walls used.

Example 1:

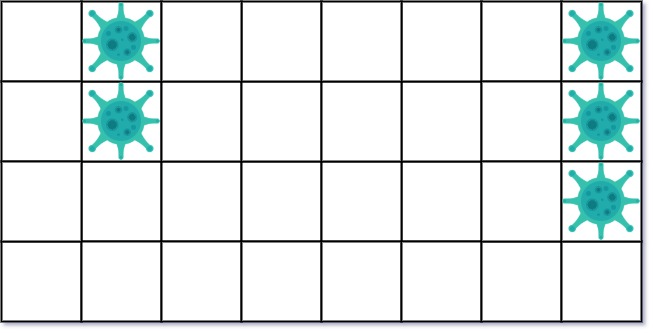
Input: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
Output: 10
Explanation: There are 2 contaminated regions.
On the first day, add 5 walls to quarantine the viral region on the left. The board after the virus spreads is:

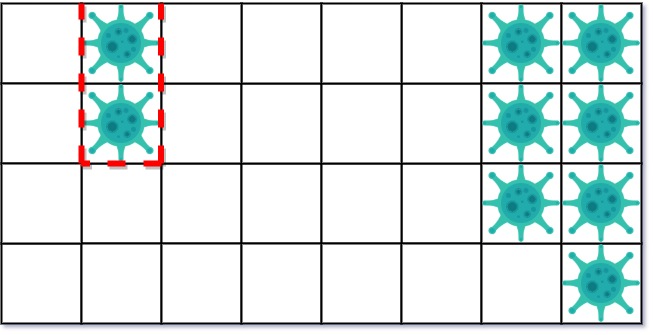
On the second day, add 5 walls to quarantine the viral region on the right. The virus is fully contained.

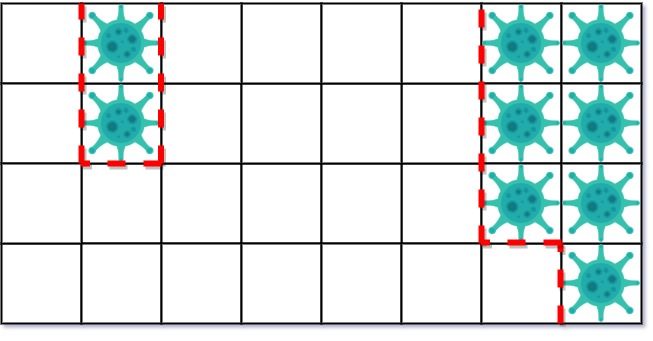
Example 2:

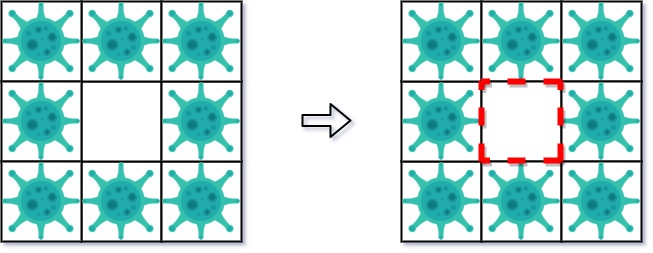
Input: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
Output: 4
Explanation: Even though there is only one cell saved, there are 4 walls built.
Notice that walls are only built on the shared boundary of two different cells.

Example 3:

Input: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]
Output: 13
Explanation: The region on the left only builds two new walls.

Constraints:

• m == isInfected.length
• n == isInfected[i].length
• 1 <= m, n <= 50
• isInfected[i][j] is either 0 or 1.
• There is always a contiguous viral region throughout the described process that will infect strictly more uncontaminated squares in the next round.

---

Analysis

  这道题目是隔离病毒，对照一下现实生活，真的挺真实的。回到题目，题目给出一个矩阵，1表示病毒，每天病毒都往四个方向扩展一格，而每天我们可以选择对连在一起的病毒群建立围墙把他们围住，使得它们无法继续感染其他的细胞，问需要多少个墙去隔离所有的感染区域。

  这道题目的信息量比较大，我们逐个来分析。第一个是病毒群，因为隔离的单位是对一群相连的病毒进行隔离，所以我们要找到相连的1，这里可以用DFS或者BFS；第二个是墙的数量，因为我们每次都是按照一个病毒群来隔离的，所以我们要记录每个病毒群如果隔离所需要墙的数量，如果某个格子是1，而周围的格子是0，那么就需要在这两个格子之间建一个墙。同时，这个墙的位置还有另一个意义，如果在第i天我们并不隔离当前的这个病毒群，那么墙的位置将会被病毒扩散，所以它还是病毒下一天扩散的位置，因此这里记录的是坐标，而不是只是一个数字。

  上面两个信息是病毒群比较基本的信息，也很容易得到，但是问题的关键是每一天我们按照什么标准去选择隔离哪个病毒群？一种很贴近现实的想法是greedy，需要隔离潜在传染数量最多的病毒群。特别注意潜在传染数最多和上面第二个围墙的数量是不一样的，比如一个值为0的格子可能被周围4个1包含，那么如果需要隔离这个病毒群则需要4个墙，但是潜在感染数量只有1个，所以这就是我们需要的第三个信息，我们只需要对上面第二个信息稍做处理即可。上面存放的是坐标，我们把所有的坐标放到一个unordered_set中去重得到数量即可。

  这样我们整体的算法就出来了，首先我们有一个大循环，一直循环直到没有活跃的病毒群。然后我们统计每一个活跃的病毒群的三个信息，加入到一个三维数组alls中，按照第三个信息从大到小排列。接着隔离第一个病毒群，这个病毒群潜在传染数是最多的。墙的总数直接加上即可，然后把这个区域里面病毒的位置都改成-1，表示已经被隔离的病毒。对剩下的病毒群，把病毒往外扩充，其实就是根据第二个信息中的坐标位置，把值都改成1。

Solution

  无。

---

Code

class Solution {
public:
    int containVirus(vector<vector<int>>& isInfected) {
        int m = isInfected.size(), n = isInfected[0].size();
        int dx[] = {-1, 0, 1, 0};
        int dy[] = {0, -1, 0, 1};
        int result = 0;
        
        while (1) {
            // get all virus group
            vector<vector<vector<int>>> all; // cells, walls, virus
            unordered_set<int> visited;
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n; ++j) {
                    if (isInfected[i][j] == 1 && !visited.count(i * n + j)) {
                        queue<int> q;
                        q.push(i * n + j);
                        
                        vector<int> walls, virus{i * n + j};
                        visited.insert(i * n + j);
                        
                        // bfs
                        while (!q.empty()) {
                            int cur = q.front();
                            q.pop();
                            for (int k = 0; k < 4; ++k) {
                                int newI = (cur / n) + dx[k];
                                int newJ = (cur % n) + dy[k];
                                if (newI < 0 || newI >= m || newJ < 0 || newJ >= n || visited.count(newI * n + newJ) || isInfected[newI][newJ] == -1) {
                                    continue;
                                }
                                if (isInfected[newI][newJ] == 0) {
                                    // add to walls
                                    walls.push_back(newI * n + newJ);
                                } else if (isInfected[newI][newJ] == 1) {
                                    // add to virus
                                    virus.push_back(newI * n + newJ);
                                    visited.insert(newI * n + newJ);
                                    q.push(newI * n + newJ);
                                }
                            }
                        }
                        
                        // add to all
                        unordered_set<int> st(walls.begin(), walls.end());
                        vector<int> cells{(int)st.size()};
                        all.push_back({cells, walls, virus});
                    }
                }
            }
            
            if (all.empty()) {
                break;
            }
            sort(all.begin(), all.end(), [](vector<vector<int>> &a, vector<vector<int>> &b) {
                return a[0][0] > b[0][0];
            });
            
            for (int i = 0; i < all.size(); ++i) {
                if (i == 0) {
                    vector<int> virus = all[0][2];
                    for (int idx: virus) {
                        isInfected[idx / n][idx % n] = -1;
                    }
                    result += all[0][1].size();
                } else {
                    vector<int> walls = all[i][1];
                    for (int idx: walls) {
                        isInfected[idx / n][idx % n] = 1;
                    }
                }
            }
        }
        return result;
    }
};

---

Summary

  这道题目是二维矩阵中比较复杂的题目，但是其基本的思想还是BFS，只不过需要根据题意去提取我们需要的信息。这道题目还有一个解题的关键是要区分需要墙的数量和能感染的数量是不一样的，意识到这个点就很容易写出代码了。这道题目的分享到这里，感谢你的支持！