LeetCode解题报告（518）-- 2128. Remove All Ones With Row and Column Flips

Problem

You are given an m x n binary matrix grid.

In one operation, you can choose any row or column and flip each value in that row or column (i.e., changing all 0‘s to 1‘s, and all 1‘s to 0‘s).

Return true if it is possible to remove all 1‘s from grid using any number of operations or false otherwise.

Example 1:

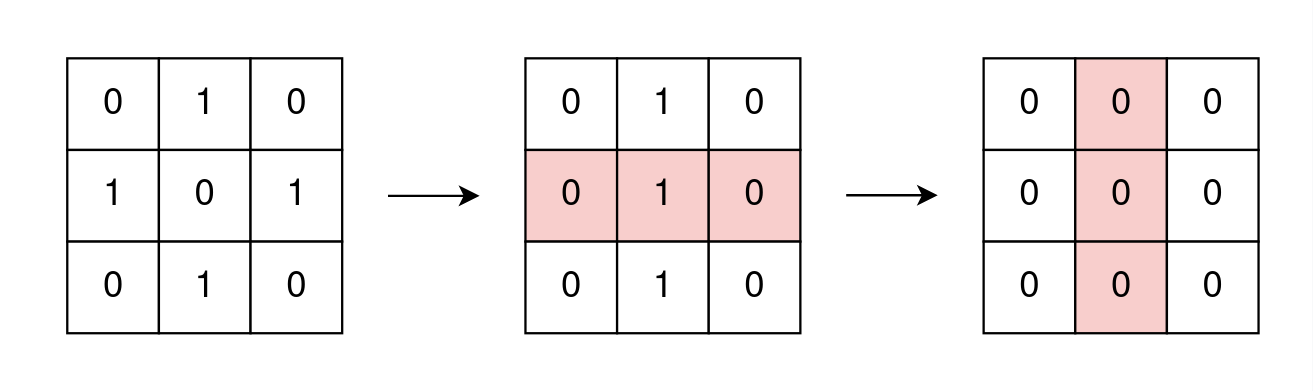
Input: grid = [[0,1,0],[1,0,1],[0,1,0]]
Output: true
Explanation: One possible way to remove all 1's from grid is to:
- Flip the middle row
- Flip the middle column

Example 2:

1
2
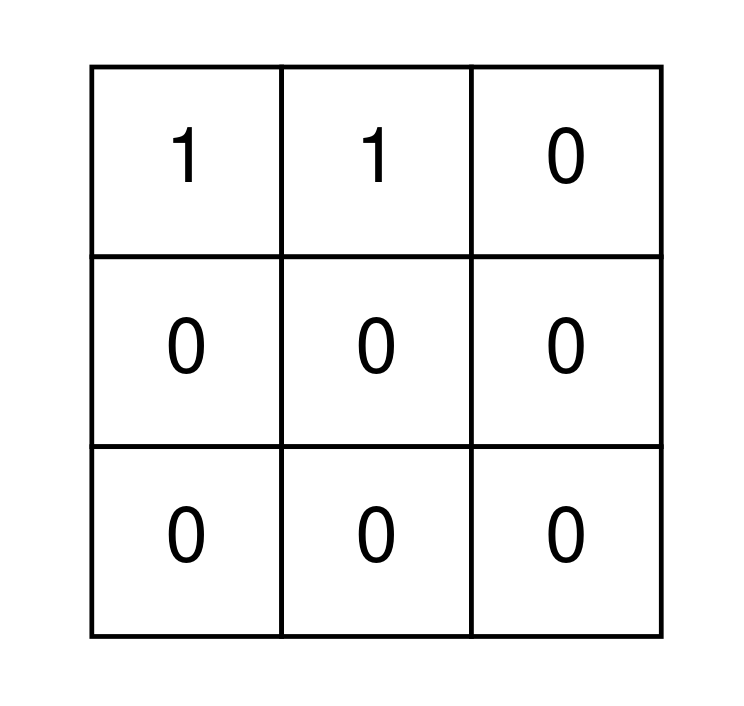
3

Input: grid = [[1,1,0],[0,0,0],[0,0,0]]
Output: false
Explanation: It is impossible to remove all 1's from grid.

Example 3:

1
2
3

Input: grid = [[0]]
Output: true
Explanation: There are no 1's in grid.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] is either 0 or 1.

Analysis

这道题是有关flipping的，题目给出一个01矩阵，每次允许的操作是翻转一行或者一列，问是否能通过若干次翻转使得整个矩阵都变成0。首先对于flipping的题目，有一个很重要的性质就是，如果某一个位置翻转了两次，那么它的值就和原来的是一样的。所以对于某一行或者某一列来说，要么不翻转，要么只翻转一次，因为翻转多于一次是多余的操作。基于这个特点，我们可以先处理第一行，对于第一行来说，如果有存在1，就把该列翻转，这样的目的是把这个1翻转成0，至于该列中其他行我先不管。处理完之后，说明我不需要再做列的翻转了，因为现在第一行全部都是0，如果对任意一列再做翻转，那么第一行就不满足了，所以我只需要看行翻转。

因为只能做行翻转，我只需要看看这一行有多少个1就可以了。如果全都是1，那么我翻转这行就可以了，如果全部为0，什么也不做。除了这两种情况之外，其他条件都是不满足的，可以直接return false。

Solution

无。

Code

class Solution {
public:
    bool removeOnes(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        
        for (int j = 0; j < n; ++j) {
            if (grid[0][j] == 1) {
                for (int i = 0; i < m; ++i) {
                    grid[i][j] = !grid[i][j];
                }
            }
        }
        
        for (int i = 0; i < m; ++i) {
            int count = 0;
            for (int j = 0; j < n; ++j) {
                count += grid[i][j];
            }
            
            if (count != 0 && count != n) {
                return false;
            }
        }
        return true;
    }
};

Summary

这道题目是flipping类型题目中非常经典的应用。做这类题目时要牢牢把握住翻转次数这个关键点。这道题目的分享到这里，感谢你的支持！