常微分方程初值问题求解

介绍

本题涉及到的是常微分方程初值问题的求解方法。求解常微分方程可以分为两类解法：（1）解析方法；（2）数值解法。前者仅限于对特殊的方程进行求解，而后者可以应用于一般方程的求解。
常微分方程初值问题的一般形式是：
$$
y^{‘} = f(x,y), x \in [x_0, b],\y(x_0) = y_0，
$$
而我们需要做的就是求解出$y=y(x)$。

分析

1.前向欧拉法

在$xy$平面上，微分方程$f(x,y) = y^{‘}$的解$y=y(x)$称作它的积分曲线。从几何角度出发，从初始点$P_0(x_0,y_0)$出发，沿该点切线方向$f(x_0,y_0)$推进到$x=x_1$上的一点$P_1$，然后再从$P1$点推进到$x=x_2$上的一点$P_2$，一直推进到$P_n$。
对于相邻的两个点$P_n$和$P_{n+1}$，有如下关系：
$$
\frac{y_{n+1} - y_n}{x_{n+1} - x_n} = f(x_n,y_n)，
$$
通过变换得到：
$$
y_{n+1} = y_n + hf(x_n,y_n)，
$$
这个方法就称为欧拉方法（前向欧拉方法）。实际上这是对常微分方程中的导数用均差来近似。若初值$y_0$已知，则可以通过递推算出$y_n$

2.后向欧拉法

如果对微分方程从$x_0$到$x_{n+1}$积分，可以得到：
$$
y(x_{n+1}) = y(x_n) + \int^{x_{n+1}}{x_n}f(t,y(t))dt，
$$
对右端的积分使用右矩形公式近似，得到：
$$
y_{n+1} = y_n + hf(x_{n+1},y{n+1})，
$$
这种方法称为后退的欧拉法（后向欧拉法）。由于等式右边含有$y_{n+1}$，所以后向欧拉法是隐式的。
隐式方法计算的时候，要使用迭代法，逐步显式化。首先使用欧拉公式提供初值，再进行迭代。
$$
y^{(0)}{n+1} = y_n + hf(x_n,y_n)\
y^{(k+1)}_{n+1} = y_n + hf(x_{n+1},y^{(1)}{n+1})
$$

3.梯形方法

在欧拉方法的基础上，对积分右端近似的方法进行改进，使用梯形求积公式近似，可以得到精度更高的计算公式，主要形式为：
$$
y_{n+1} = y_n + \frac{h}{2}[f(x_n,y_n) + f(x_{n+1}, y_{n+1})]，
$$
这种方法被称为梯形方法，由于等式右端同样含有$y_{n+1}$，因此这种方法也是隐式的。求解的方法同后向欧拉类似，由欧拉方法给出初值，再逐步显式化。
$$
y^{(0)}{n+1} = y_n + hf(x_n,y_n) \
y^{(k+1)}_{n+1} = y_n + \frac{h}{2}[f(x_n,y_n) + f(x_{n+1},y^{(k)}{n+1})], k = 0,1,2,\dots
$$

4.改进欧拉方法

梯形方法给我们提供了一种获得更高精度的算法，但是其计算量是庞大的，因为每步迭代都需要重新计算$f(x,y)$的值。这里给出了一种思路：先使用欧拉方法求得一个初步的近似值$\overline y_{n+1}$,\，称为预测值，但是这个预测值的精度可能会很差，因此需要校正。这里使用梯形公式对其进行校正，得到一个校正值$y_{n+1}$。这种预测-校正系统称为改进的欧拉公式：
$$\begin{cases}
预测 \overline y_{n+1} = y_n + hf(x_n,y_n)，\
校正 y_{n+1} = y_n + \frac{h}{2}[f(x_n,y_n) + f(x_{n+1}, \overline y_{n+1})]
\end{cases}$$

代码实现

1.前向欧拉法

根据上述推导的公式，编写matlab代码：

% 前向欧拉方法
function [x,y] = Euler(a, b, y0, h)
    x(1) = a;
    y(1) = y0;
    n = (b - a) / h;
    for i = 1:n
        x(i+1) = x(i) + h;
        y(i+1) = y(i) + h * myFun(x(i),y(i));
    end
end

function f = myFun(x, y)
    f = y - 2 * x / y;
end

2.后向欧拉法

根据上述推导的公式，编写matlab代码：

% 后向欧拉方法
function [x,y] = EulerBackward(a, b, y0, h)
    n = (b - a) / h;
    x = zeros(1, n);
    x(1) = a;
    y(1) = y0;

    for i = 1:n
        x(i+1) = x(i) + h;
        yt = y(i) + h * myFun(x(i), y(i)); % 使用欧拉公式给出迭代初值
        finished = 0; % 初始化
        while ~finished
            y(i+1) = y(i) + h * myFun(x(i+1), yt);
            finished = (abs(y(i+1) - yt) < 0.000001);
            yt = y(i+1);
        end
    end
end

function f = myFun(x, y)
    f = y - 2 * x / y;
end

3.梯形方法

根据上述推导的公式，编写matlab代码：

% 梯形方法
function [x,y] = Trapezoid(a, b, y0, h)
    n = (b - a) / h;
    x = zeros(1, n);
    y(1) = y0;
    x(1) = a;

    for i = 1:n
        x(i+1) = x(i) + h;
        yt = y(i) + h * myFun(x(i), y(i)); % 使用欧拉方法提供迭代初值
        finished = 0; % 初始化
        while ~finished
            y(i+1) = y(i) + (h/2) * (myFun(x(i), y(i)) + myFun(x(i+1), yt));
            finished = (abs(y(i+1) - yt) < 0.000001);
            yt = y(i+1);
        end
    end
end

function f = myFun(x, y)
    f = y - 2 * x / y;
end

4.改进欧拉方法

根据上述推导的公式，编写matlab代码：

% 改进欧拉方法
function [x,y] = EulerImproved(a, b, y0, h)
    n = (b - a) / h;
    x = zeros(1, n);
    y(1) = y0;
    x(1) = a;

    for i = 1:n
        x(i+1) = x(i) + h;
        yt = y(i) + h * myFun(x(i), y(i)); % 预测
        y(i+1) = y(i) + (h/2) * (myFun(x(i), y(i)) + myFun(x(i+1), yt)); % 校正
    end
end

function f = myFun(x, y)
    f = y - 2 * x / y;
end

小结

运行上述各方法的代码后，分别对其进行简单的数值实验，结果如下：
前向欧拉方法结果：

后向欧拉方法结果：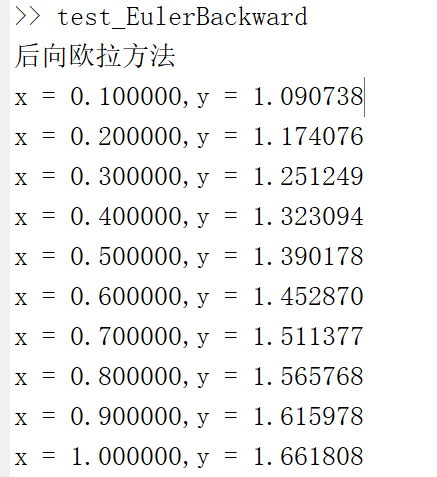

梯形方法结果：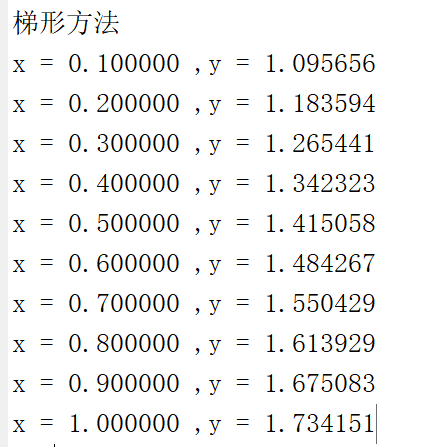

改进欧拉方法结果：

由上述几种方法可以看出，前向欧拉方法和后向欧拉方法的误差是比较大的，改进的欧拉方法精度比欧拉法要好，而在四种方法中，梯形方法拥有更高的精度。但是从计算复杂度而言，欧拉法是比较简单的。考虑到数值稳定性的问题，有时可以使用后向欧拉方法来保证数值的稳定性。综合计算复杂度和精度而言，个人认为改进欧拉方法是一个比较好的折中方案。

参考资料：

1.数值分析（第5版）李庆扬，王能超，易大义编