Halo

A magic place for coding

0%

LMS--最小均方法

Posted on Edited on Valine:

Intro

  最小均方法，Least Mean Square（简称LMS），是一种通过最小化误差的机器学习算法。它是机器学习常用的算法之一，通常结合梯度下降法来求解出最优的参数。

LMS算法

loss function

所谓均方，就是误差的平方的均值。LMS训练法则，可以简述为以下式子，通常也叫做代价函数（cost function）：
$$
J(w)=\frac12\sum^m_{i=1}{h(x^{(i)})-y^{(i)}}^2
$$
其中，$h(x^{(i)})$为学习网络的输出信号，$y^{(i)}$为导师信号。

Gradient Descent

  我们的目的就是要通过某种方法，来最小化这个代价函数。通常使用的方法是梯度下降法（gradient descent），因为对于凸优化问题而言，导数值为0的地方就是全局极小值。所以我们可以利用梯度来指引我们向极小值处走近。

  梯度下降法的更新规则为：
$$
\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta)
$$
  **注意:**这里的$\theta_j$的更新是同步的（即是用相同的$J(\theta)$），也就是说，更新完所有的$\theta_j（j=0,\dots,n）$后，才算下一个梯度。

  然后我们推导梯度的计算：
$$
\begin{aligned}
\frac{\partial}{\partial\theta_j}J(\theta) &= \frac{\partial}{\partial\theta_j}\frac{1}{2}(h_\theta(x) - y)^2 \
&=2 \cdot \frac{1}{2}(h_\theta(x) - y) \cdot \frac{\partial}{\partial\theta_j}(h_\theta(x) - y)
\
&=(h_\theta(x) - y) \cdot\frac{\partial}{\partial\theta_j}(\sum^n_{i=0}\theta_ix_i-y) \
&=(h_\theta(x)-y)x_j
\end{aligned}
$$
  因此对于某一个样例来说，其更新规则为：
$$
\theta_j:=\theta_j+\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}
$$
  可以看出，当预测值$h_\theta(x^{(i)})$和真实值$y^{(i)}$相等时，该参数并不会更新；而当它们不相等时，参数会按照他们的difference来更新参数，这样从直观上来说也是合理的。

  梯度下降法给我们提供了一种求代价函数极小值的方法，它有很多变种，下面就介绍几种常用的方法。特别注意，仅当我们面对的是一个凸优化问题，梯度下降法才能够保证让我们找到全局最优解。

Batch Gradient Descent

  批梯度下降法，其本质是每一轮迭代使用整个训练集去更新权重，即考虑了整体样本的梯度。其算法伪代码为：

$Repeat ;Until ;convergence; {$

$ \quad \theta_j:=\theta_j+\alpha\sum^m_{i=1}(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)};;(for ; every; j)$

$}$

Stochastic Gradient Descent

  随机梯度下降法，其本质是每次迭代只用一个样例去计算梯度，更新参数。相比起批梯度下降法，随机梯度下降法大大提高了计算效率。从理论上说，SGD能让我们更快地找到最佳的参数，但是它有可能无法收敛到极小值，而是在极小值附近波动。但实际情况时，对于极小值附近的值也是对极小值的一个很好的近似，因此在数据集较大的情况下，SGD的实际效果是优于BGD的。其算法伪代码为：

$Loop ; {$

$ \quad for ;i=1 ;to;m, ; {$

$ \quad \quad \theta_j:=\theta_j+\alpha(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)};;(for ; every; j)$

$ \quad }$

$ } $

实例

  我们以拟合一条直线作为例子，以下给出一些前提定义：

  • 训练样例$X_i(a_i, b_i)$，$i = 1,2,…,n$，$n$为样本大小
  • 导师信号$D=[d_1, d_1,…,d_i]$，$i = 1,2,…,n$，$n
    $为样本大小
  • $h(X_i)$是在假设$h$下预测得到的预测值
  • 权值矩阵$W=[w_0,w_1]$
  • 目标函数$w_0x+w_1y$
  • 学习率（步长）$\eta$4，$0\lt \eta \lt 1$
  • 更新法则：$W(n+1) = W(n) + \eta * X_i * (d_i - h(X_i))$

  我们输入的数据是一系列的点，以及导师信号D（target value）。我们期望的输出是描述这个直线的权值矩阵$W=[w_0,w_1]$。

初始化变量

初始化一些变量，其含义注释有描述。

1
2
3
4
5
6
7
import numpy as np
a = 0.1 # 0 < a < 1
X = np.array([[-1, 1], [-1, 0], [0, 1], [0, 0]]) # Input matrix
D = np.array([1, 1, 1, 0]) # target value
W = np.array([0, 0]) # Weight vector
expect_e = 0.005 # Expected Error
maxtrycount = 20

激活函数

激活函数（Activation Function）可以视为一个神经元对输入的反馈。举个简单的例子来帮助大家理解，我们听到一个消息，可能会激动，也可能不会激动。这个激活函数就是来判断我们是否会激动的函数。具体看，假如我们得知的是考试分数，80分以下我们就不会激动，80分以上我们就激动，那么这个激活函数就可以写为：

1
2
3
4
5
def sgn(x):
	if x > 80:
	   激动
	else:
	   不激动

那么在我们这个例子中，我们要确定一条直线，那么我们给出的是这个点在线的上方（1）还是下方（0）。

1
2
3
4
5
6
# Activation Function
def sgn(v):
  if v > 0:
    return 1
  else:
    return 0

输出信号

在每一个神经元我们要输出预测值，这是根据上面给出的激活函数得出的。

1
2
def get_v(W, x):
  return sgn(np.dot(W.T, x))

dot是矩阵乘法，W.T是代表W的转置。因此np.dot(W.T, x))是一个实数。

计算误差

误差是预测值与导师信号之差。

1
2
def get_error(W, x, d):
  return d - get_v(W, x)

更新权重

按照上面给出的权重更新公式来计算更新后的权重。

1
2
3
4
5
6
7
# Update Weights
'''
  W(n + 1) = W(n) + a * X(n) * e
'''
def getNewWeight(oldW, d, x, a):
  e = get_error(W, x, d)
  return (oldW + a * x * e, e)

返回一个pair，第一部分是更新后的参数，用于赋值给W，第二部分是当前这个样本$X_i$的误差，用来计算均方。

训练过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Training
count = 0
while True:
  error = 0
  i = 0
  for xn in X:
    W, e = getNewWeight(W, D[i], xn, a)
    i += 1
    error += pow(e, 2) ## calculate MES
  error /= float(i)
  count += 1
  print(u"Weights after %d updates: " %count)
  print(W)

  print(u"Error: %f"%error)
  if error < expect_e or count >= maxtrycount:
    break

  这里的训练过程我们称为批量的，因为每一个循环都对所有的样本进行训练，然后调整权重。这种做法开销比较大，但是精度较高。

测试部分

我们先对训练数据进行测试，然后再对两个单独的例子进行测试。

1
2
3
4
5
6
# Test
print("Begin Test")
test = np.array([2, 3])
print("X%s and W%s => %d"%(test, W.T, get_v(W, test)))
test = np.array([-2, -1])
print("X%s and W%s => %d"%(test, W.T, get_v(W, test)))

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
'''
  Author: LeungYukshing
  Algorithm: Least Mean Squares
  observed is true value, predicted is predicted sample value
  MES = [(observed[0] - predicted[0]) * (observed[0] - predicted[0]) + ...
          + (observed[n] - predicted[n]) * (observed[n] - predicted[n])] / n
'''

'''
  UpperCase indicates a matrix or an array
  LowerCase indicates a value
'''

'''
  Learning Rate: a
  Too large: converge fastly, less stable
'''

import numpy as np
a = 0.1 # 0 < a < 1
X = np.array([[-1, 1], [-1, 0], [0, 1], [0, 0]]) # Input matrix
D = np.array([1, 1, 1, 0]) # target value
W = np.array([0, 0]) # Weight vector
expect_e = 0.005 # Expected Error
maxtrycount = 20

# Activation Function
def sgn(v):
  if v > 0:
    return 1
  else:
    return 0

def get_v(W, x):
  return sgn(np.dot(W.T, x))

def get_error(W, x, d):
  return d - get_v(W, x)

# Update Weights
'''
  W(n + 1) = W(n) + a * X(n) * e
'''
def getNewWeight(oldW, d, x, a):
  e = get_error(W, x, d)
  return (oldW + a * x * e, e)

# Training
count = 0
while True:
  error = 0
  i = 0
  for xn in X:
    W, e = getNewWeight(W, D[i], xn, a)
    i += 1
    error += pow(e, 2) ## calculate MES
  error /= float(i)
  count += 1
  print(u"Weights after %d updates: " %count)
  print(W)

  print(u"Error: %f"%error)
  if error < expect_e or count >= maxtrycount:
    break

print("Final Weight: ", W.T)

# Output
for xn in X:
  print("Xn%s and W%s =>%d"%(xn, W.T, get_v(W, xn)))

# Test
print("Begin Test")
test = np.array([2, 3])
print("X%s and W%s => %d"%(test, W.T, get_v(W, test)))
test = np.array([-2, -1])
print("X%s and W%s => %d"%(test, W.T, get_v(W, test)))

分析

先给出程序运行结果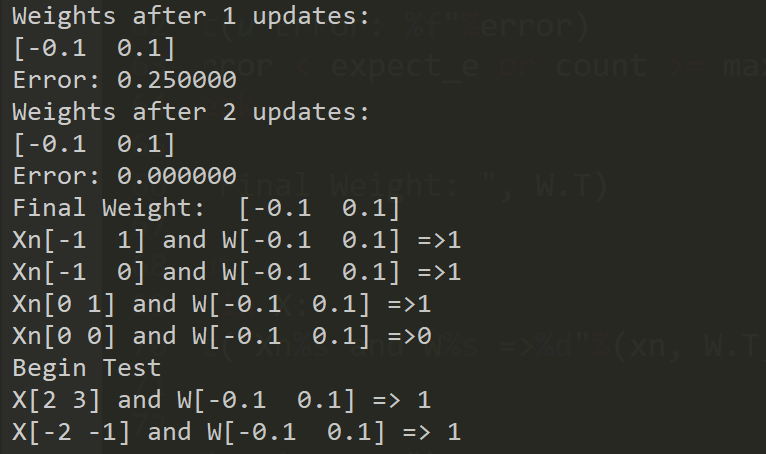：LMS结果

可以看出，实际上我们训练出来的直线是y=x。从拟合的角度看，我们根据给出的一系列点，最后拟合出一条直线。从分类的角度看，这条直线将二维平面分成两部分，在直线上方的标记为1，在直线下方的标记为0。

在这个例子中，训练两次后就已经满足了我们期望的误差，这是因为我给出的点是比较好的，很容易识别出来。对于其他的直线和数据集，可能需要多次的训练才能得到结果。

总结

LMS算法本质上是给我们提供了一种判断方法，判断当前的权值对于实际预测的准确性。机器学习的任务就是去极小化这个误差。先来看看这里用到的更新方法：$W(n+1) = W(n) + \eta * X_i * (d_i - h(X_i))$

我们这样理解：

  • 当$(d_i - h(X_i))=0$时，权值不会改变。这说明当导师信号和我们预测的信号一致时，我们就认为当前的分类是正确的，无需做出改变。
  • 当$(d_i - h(X_i))$为正时，说明预测值比导师信号要小，所以需要在原权值的基础上增加一定的比例。反之亦然。
  • 当$X_i=0$时，权值不会改变。这说明当这个特征$X_i$没有出现时，它的权值是不会因为误差而改变的。

当然，在实际应用中，我们更多使用的是梯度下降法，这会在之后的博客中和大家分享，这里就只分析LMS算法。谢谢您的支持！

Welcome to my other publishing channels