Halo

A magic place for coding

0%

LeetCode解题报告（373) -- 304. Range Sum Query 2D - Immutable

Posted on Edited on Valine:

Problem

Given a 2D matrix matrix, handle multiple queries of the following type:

  1. Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

  • NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
  • int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Example 1:

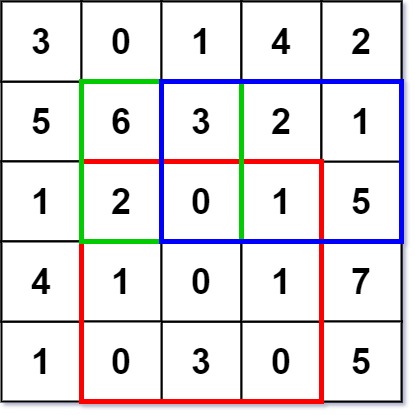
Example1

1
2
3
4
5
6
7
8
9
10
11
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 200
  • -105 <= matrix[i][j] <= 105
  • 0 <= row1 <= row2 < m
  • 0 <= col1 <= col2 < n
  • At most 104 calls will be made to sumRegion.

Analysis

  题目给出了一个矩阵，要求实现一个方法，指定子矩阵的左上角和右下角坐标，求出子矩阵的和。一开始我采用的思路是调用该方法时才去计算，这样显然是不行的，会超时。所以就必须用空间换取时间了，要在初始化的时候就预先处理好。但是我们究竟要存储什么信息，才能在调用时快速计算出子矩阵的和呢？

  这里涉及到一个概念叫前缀和。对于一维数组，如果知道前缀和的话，计算[i, j]之间的和就是presum[j] - presum[i - 1]。这个思路同样适用于二维数组，不过计算的时候就复杂一些。定义m[i][j]是以(0,0)为左上角，(i,j)为右下角的子矩阵的和，其计算方式为m[i][j] = m[i][j - 1] + m[i - 1][j] - m[i - 1][j - 1] + matrix[i - 1][j - 1]。简单解释一下，m[i][j - 1]和m[i - 1][j]都是之前求出来的，两者相加后，重叠的面积是m[i - 1][j - 1]，再加上新增的matrix[i - 1][j -= 1]就是当前的值了。

  前缀和知道怎么求了，然后我们来看如果用前缀和求出答案。其实也是通过几个前缀和之间运算得到，二维矩阵中画图就很容易明白了。这里的计算方式为：m[row2 + 1][col2 + 1] - m[row1][col2 + 1] - m[row2 + 1][col1] + m[row1][col1]。

Solution

  为了统一代码处理，前缀和的二维矩阵都开多了一列和一行，便于处理边界情况。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class NumMatrix {
public:
    NumMatrix(vector<vector<int>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) {
            return;
        }
        m.resize(matrix.size() + 1, vector<int>(matrix[0].size() + 1, 0));
        
        for (int i = 1; i <= matrix.size(); i++) {
            for (int j = 1; j <= matrix[0].size(); j++) {
                m[i][j] = m[i][j - 1] + m[i - 1][j] - m[i - 1][j - 1] + matrix[i - 1][j - 1];
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return m[row2 + 1][col2 + 1] - m[row1][col2 + 1] - m[row2 + 1][col1] + m[row1][col1];
    }
private:
    vector<vector<int>> m;
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */

Summary

  这道题目的本质思路就是二维矩阵的前缀和，包括如何构建前缀和以及如何通过前缀和来求出答案。推理运算公式时可以多点画图，找出重叠的地方，这样就很好理解了。这道题目的分享到这里，感谢你的支持！

Welcome to my other publishing channels