Halo

A magic place for coding

0%

逻辑回归--LogisticRegression

Posted on Edited on Valine:

Intro

  Logistic Regression，逻辑回归，实质上解决的是一个分类问题（我们之前说过，机器学习主要解决两类问题：回归和分类）。那为什么它又叫Regression呢？这是因为它用到了一个非线性函数——sigmoid函数，它给出的结果是一个概率值，而不是一个用于直接确定分类的离散值。下面我们就来仔细看看这个非常常用的分类算法。

原理

  首先我们还是基于传统的线性回归（Linear Regression）去思考一个分类问题，假设我们的模型预测值是$h_\theta(x)$，这个值的范围是不确定的，我们很难去找到一个不错的阈值去划分两类（因为模型的输出会受数据分布的影响，0.5并不是一个很科学的阈值）。这个时候我们就需要将$h_\theta(x)$的值压缩到一个相对小的区间中，最理想的情况就是压缩到[0,1]中，这样输出的就可以是一个概率了。

  幸运的是，我们能找到这样的函数——Sigmoid function（Logistic function）。它的曲线是这样的：

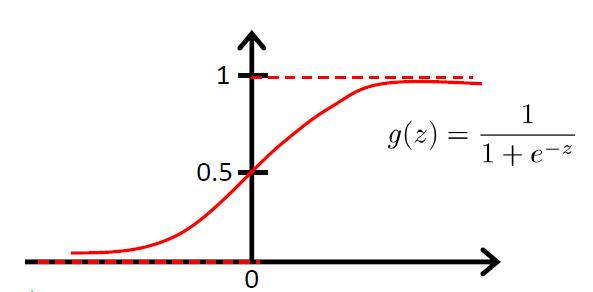
  从sigmoid的图像中我们可以看到一些我们想要的特性：

  • 当$z\rightarrow\infty$时，$g(z)\rightarrow1$；当$z\rightarrow -\infty$时，$g(z)\rightarrow 0$

  • $g(z)$的值被限制在了[0, 1]

  • sigmoid是光滑的，他的导数也是很容易求得：
    $$
    \begin{aligned}
    g^{‘}(x) &= \frac{d}{dz}\frac{1}{1+e^{-z}} \
    &=\frac{1}{(1+e^{-z})^2}(e^{-z}) \
    &= \frac{1}{(1+e^{-z})} \cdot(1 - \frac{1}{(1+e^{-z})}) \
    &= g(z)(1-g(z))
    \end{aligned}
    $$

  于是模型的输出就变为：
$$
h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}
$$
  建立好模型后，我们的工作就是需要找到这个最佳的$\theta$。之前我们用的是LMS，但是这里使用LMS得到的并不是一个凸函数，我们需要换另一种方式——最大似然法。

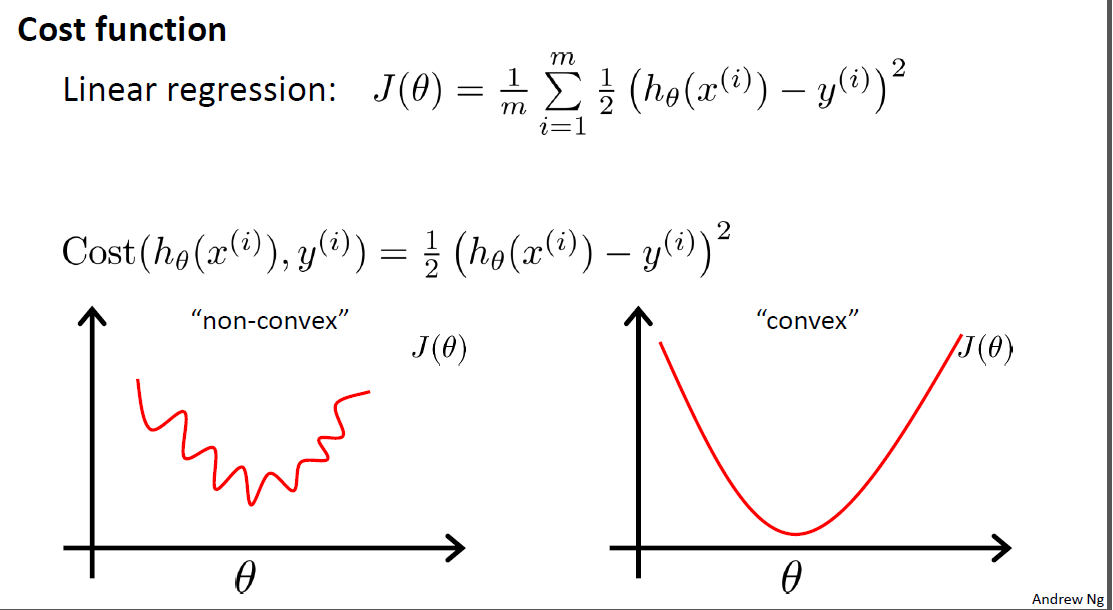
  最大似然法的思路是：我已经知道了若干个测试结果，我需要找出一组参数$\theta$，使得它们能够很好地模拟出这些测试结果。将每一个模拟的概率乘起来，极大化这个概率，我们就能得到最好的$\theta$。下面我们就来表示这些概率。

  首先我们假设：
$$
\begin{aligned}
&P(y=1|x;\theta)=h_\theta(x) \
&P(y=0|x;\theta)=1-h_\theta(x)
\end{aligned}
$$
  从条件概率的角度看，这两条式子的意思是：对于给定的$x$和$\theta$，模型的输出就是$x$属于类别1的概率。这个可以看作一个二项分布问题，所以我们可以将两条式子合并到一起：
$$
p(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y}
$$
  假设$m$个训练样本都是相互独立的，我们可以应用最大似然估计：
$$
\begin{aligned}
L(\theta) &= p(\hat{y}|X;\theta) \
&= \prod_{i=1}^mp(y^{(i)}|x^{(i)};\theta) \
&= \prod_{i=1}^m(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}
\end{aligned}
$$
  一般来说，我们都不会直接极大化$L(\theta)$，而是极大化它的对数：
$$
\begin{aligned}
l(\theta) &= logL(\theta) \
&= \sum_{i=1}^my^{(i)}logh(x^{(i)}) + (1-y^{(i)})log(1-h(x^{(i)}))
\end{aligned}
$$
  极大化$l(\theta)$对我们来说就不是一件困难的事了，我们可以简单地使用GA（Gradient Ascend）。（特别注意，因为这里是要极大值，所以使用的Gradient Ascend）。推导过程如下：
$$
\begin{aligned}
\frac{\partial}{\partial\theta_j}l(\theta) &= (y\frac{1}{g(\theta^Tx)} -(1-y)\frac{1}{1-g(\theta^Tx)})\frac{\partial}{\partial\theta_j}g(\theta^Tx) \
&= (y\frac{1}{g(\theta^Tx)} -(1-y)\frac{1}{1-g(\theta^Tx)})g(\theta^Tx)(1-g(\theta^Tx))\frac{\partial}{\partial\theta_j}\theta^Tx \
&= (y(1-g(\theta^Tx))-(1-y)g(\theta^Tx))x_j \
&= (y-h_\theta(x))x_j
\end{aligned}
$$
  因此，最后的更新规则为：
$$
\theta_j := \theta_j+\alpha(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)}
$$
  有没有发现很眼熟？这个更新规则和LMS的更新规则是一样的！但是两者从本质上是不同的，这里的$h_\theta(x^{(i)})$是sigmoid函数。

  至此，Logistic Regression的原理推导就完成了！大家最好能够自己手动推导一次。

实战

  这里我用逻辑回归来预测疝气病马的存活问题。数据集来自UCI：传送门

数据预处理

  之前的博客给过处理UCI数据的一些代码模板，需要特别注意，这次的数据存在许多缺漏，因此我们需要手动处理一下。

  这里也简单地介绍一下如何处理缺失数据。处理缺失数据是特征工程一个很重要的部分，因为随便填补或删除会使得数据有可能加入了人为的噪声，所以我们需要有多种方法去填补。以下是几个典型的方法：

  • 使用可用特征的均值（或众数）来填补缺失值；
  • 使用特殊值来填补缺失值，如-1（相当于添加了一个新的类别）
  • 直接忽略掉有缺失值的样本（对于缺失属性较多的样本可以这样做）
  • 使用相似样本的均值填补缺失值
  • 使用其他机器学习的方法预测缺失值（如使用随机森林来预测，相当于根据已知特征来预测缺失的特征）

  对于这个样本，我的处理主要有两个：

  • 使用0来填补缺失值，因为0对回归系数不会有影响，不会添加人为的bias。
  • 如果某个样例的标签（label）缺失，则直接丢弃这个样例。（相当于不知道答案就不用做题）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import numpy as np

frTrain = open('./horse_colic_data.txt')#训练数据
frTest = open('./horse_colic_test.txt')#测试数据
trainSet=[]
for line in frTrain.readlines():
    currLine=line.strip().replace('?', '0').split('\t')
    temp = currLine[0].split(' ')
    lineArr=[]

    for i in range(22):
        if i == 2:
            continue
        else:
            lineArr.append(float(temp[i]))
    if (temp[22] == '1'):
        lineArr.append(1)
    else:
        lineArr.append(0)
    #print(lineArr)
    trainSet.append(lineArr)
trainSet.pop(132)
print(type(trainSet))
np.savetxt('processedHorseColicTraining.txt', trainSet, fmt='%.6f', delimiter='\t')

testSet = []
for line in frTest.readlines():
    currLine=line.strip().replace('?', '0').split('\t')
    temp = currLine[0].split(' ')
    lineArr=[]

    for i in range(22):
        if i == 2:
            continue
        else:
            lineArr.append(float(temp[i]))
    #print(type(temp[22]))
    if (temp[22] == '1'):
        lineArr.append(1)
    else:
        lineArr.append(0)
    #print(len(lineArr))
    testSet.append(lineArr)
    np.savetxt('processedHorseColicTest.txt', testSet, fmt='%.6f', delimiter='\t')

构建Logistic回归分类器

  定义sigmoid函数，使用梯度上升法求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from numpy import *
import pandas as pd
import numpy as np
def loadDataSet():
    file = './processedHorseColicTraining.txt'
    df = np.loadtxt(file)
    dataMat = df[:, 0:-1]
    #dataMat = np.insert(dataMat, 0, 1, axis=1)
    labelMat = df[:, -1]
    return dataMat, labelMat

dataMat, labelMat = loadDataSet()
print(dataMat.shape)

def sigmoid(x):
    return 1/(1+exp(-x))

def gradientAscent(dataMatIn, classLabels):
    m,n=shape(dataMatIn)
    print(n)
    classLabels = np.array([classLabels]).T
    weights = np.ones((n,1))
    alpha = 0.001
    max_iter = 500

    for _ in range(max_iter):
        h = sigmoid(np.dot(dataMatIn, weights))
        error = classLabels - h
        weights += alpha * np.dot(dataMatIn.T,error)
    return weights

随机梯度上升法

  这里试用随机梯度上升法，每次梯度更新仅用到了一个样例。

1
2
3
4
5
6
7
8
9
def stochasticGradientAscent(dataMatIn, classLabels):
    m, n = np.shape(dataMatIn)
    alpha = 0.01
    weights = np.ones(n)
    for idx in range(m):
        h = sigmoid(sum(dataMatIn[idx] * weights))
        error = classLabels[idx] - h
        weights += alpha * error * dataMatIn[idx]
    return weights

构建输出部分

  前面提到，Logistic Regression的输出是一个概率值，我们需要将这个概率值转化为一个类别，用0.5作为阈值是一个不错的选择。

1
2
3
4
5
6
def classifyVector(inX, trainWeights):
    prob = sigmoid(sum(np.dot(inX,trainWeights)))
    if prob > 0.5:
        return 1
    else:
        return 0

测试

  使用测试集来评估模型的效果。同时还可以对比两种不同的梯度上升法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
test_file = './processedHorseColicTest.txt'
df_test = np.loadtxt(test_file)
testDataMat = df_test[:, 0:-1]
testLabelMat = df_test[:, -1]
print(testDataMat)


import time
start = time.clock()

result2 = advancedStochasticGradientAscent(dataMat, labelMat, 500)

end = time.clock()
print (end - start)

errorCount = 0;numTestVec = 0;
[rows, cols] = testDataMat.shape

for i in range(rows):
    numTestVec += 1
    if classifyVector(array(testDataMat[i, :]), result2) != int(testLabelMat[i]):
        errorCount += 1

print(errorCount, numTestVec)
errorRate = (float(errorCount) / numTestVec)
print('the error rate of this test is: %f' % errorRate)

  测试结果：

  • 随机梯度上升法，错误率约37%

  • 常规的梯度上升法，错误率约29%

    考虑到整个数据集的缺失率在30%左右，这个错误率也是可以接受的范围了。

使用Sklearn

  使用Sklearn构建LogisticRegression模型非常简单，只需要定义几个变量就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from sklearn.linear_model import LogisticRegression
import numpy as np

def colicSKlearn():
    file = './processedHorseColicTraining.txt'
    df = np.loadtxt(file)
    dataMat = df[:, 0:-1]
    labelMat = df[:, -1]

    test_file = './processedHorseColicTest.txt'
    df_test = np.loadtxt(test_file)
    testDataMat = df_test[:, 0:-1]
    testLabelMat = df_test[:, -1]

    classifier1 = LogisticRegression(solver='liblinear', max_iter=20).fit(dataMat, labelMat)
    classifier2 = LogisticRegression(solver='sag', max_iter=5000).fit(dataMat, labelMat)

    test_accuracy = classifier1.score(testDataMat, testLabelMat) * 100
    print('Accuracy: %f%%' % test_accuracy)

if __name__ == '__main__':
    colicSKlearn()

  这里简单解释一下模型的参数：

  • solver：优化算法。选项为：
    • liblinear：坐标下降法
    • lbfgs：拟牛顿法，使用二阶导数来优化（海森矩阵）。
    • newton-cg：牛顿法的一种。
    • sag：随机平均梯度下降
    • saga：SAG的加速版本

  测试的结果正确率为73.529412%，似乎比我们自己写的要好一点点。

总结

  Logistic Regression是机器学习中分类算法的基础，应用的范围非常广，实际效果也非常不错。一定要注意区分它和线性回归，它的数学原理推导部分是重点！至于实际应用，调用sklearn的模型就可以了。

Welcome to my other publishing channels