Halo

A magic place for coding

0%

单个感知器的原理及简单实现

Posted on Edited on Valine:

Intro

  这里我将介绍一下神经网络中最基本的组成部分——单个感知器（神经元）。它是组成神经网络最基本的单元，我们通过弄清楚单个神经元如何工作，最终构建起一个简单的神经网络。因此，这篇博客的重点在于单个神经元。

原理

  这里我们讨论的是最简单的神经元：

  • 多个输入（$X=(x_1,x_2,\cdots,x_n)$）
  • 单个输出$y^{‘}$（这里使用$y^{‘}$代表模型预测的结果，$y$代表样本真实的标签值）。
  • 对于多个输入，每个输入的重要性是不一样的，因此对应每个输入，我们还给他们分配权重$W=(w_1,w_2,\cdots,w_n)$。
  • 阈值$\theta$
  • 激活函数$f$

  以上就是单个神经元所包含的最基本的要素。然后我们就来看它的工作原理。对于输入$X$和权重$W$，我们计算出他们的点乘结果$Z$。但是要注意，这个$Z$本身并不是我们想要的结果，我们需要做的是一个分类，因此就需要给出一个分类的标准，也就是阈值$\theta$。激活函数的工作就是：当$Z<\theta$，感知器输出0，当$Z \geq \theta$，感知器输出1。这样就完成了我们很简单的一个分类操作。

  以上只是一个感知器的正向工作部分，但它之所以能学习到规律，是因为下面要讲的反馈部分。

  需要注意，上面的各个变量中，$W$和$\theta$是不知道的，其他都是用户定义或者是训练集给出的。那么这个感知器的任务就是学习到一个比较好的$W$和$\theta$。首先我们随机初始化$W$和$\theta$（一般是比较小的随机数），然后通过一次正向的工作，得出一个预测结果。当然，这个预测结果很大可能是不正确的，因此这里需要对$W$和$\theta$进行修正。那么这个修正的根据是什么呢？当然就是训练集提供的标签值，也就是导师信号。

  这个感知器一开始就是一个无知的学生，通过不断地试错，计算出结果，与导师的答案对比，不断更改自己的$W$和$\theta$，以求最后达到一个不错的结果。那么我们就会很关心这个更新的规则：
$$
W(n+1) = W(n) + \Delta W(n) * x_i\
\theta(n+1) = \theta(n) + \Delta W (n)\
\Delta W(n) = \eta * (y - y^{‘})
$$
注意，这里的$x_i$是一个向量，$W(n+1)$和$W(n)$都是向量。

  当预测结果与标签值一致时，$y-y^{‘}$为0，权值$W$无需更新。

实战

  下面我们就用一个实例来看看一个感知器能做些什么。感知器最常见的工作就是对数据进行分类。这里我们尝试用一个感知器去做一个花的分类。输入的是花的一些性质，输出的是花的分类。

获取数据集

  这里用到的是Iris数据集：传送门。它是UCI提供的机器学习训练数据集。我们可以手动下载到本地，也可以用sklearn导入，这里使用的本地数据。

  点击【Data Folder】，进入【iris.data】并下载，保存为.csv文件。

  然后调用pandas库读入数据。

1
2
3
4
# Read Data
file = './iris.data.csv'
df = pd.read_csv(file, header=None)
df.head(10)

  查看前10条数据：

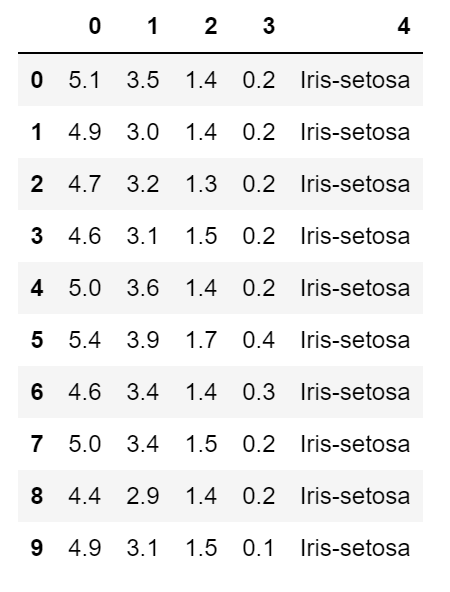
iris数据概览

处理数据

  我们获得数据后，要提取出我们需要的数据。为了实验方便，我们这里的感知器解决的是线性可分问题，也就是两个输入，一个输出。这样可以在二维平面上很清晰地展现出来。

  我们使用前100条数据作为训练集，我们可以通过查看数据介绍来提取必要的信息。

iris数据介绍

  我们使用第5列（花的类别）作为数据标签值，使用第1列（花萼长度）和第三列（花瓣长度）作为数据的输入。注意标签值的转化，将处理字符串转别为处理一个布尔变量（0，1表示）。

1
2
3
4
5
6
7
8
9
10
11
12
13
# Extract the first 100 data record

# y is the column 4
y = df.loc[0:100, 4].values
# print(y)

# Convert string to int value
y = np.where(y == 'Iris-setosa', -1, 1)
#print(y)

# X is the column 0 and 2
X = df.loc[0:100, [0, 2]].values
# print(X)

  这里我们还可以通过可视化工具来初步观察一下数据的特点。

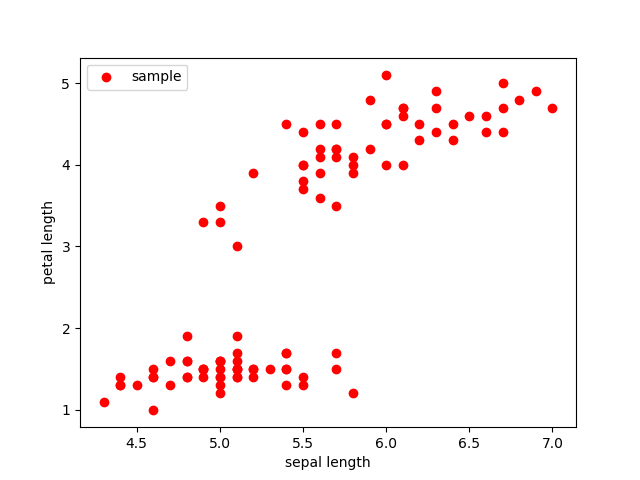
iris数据可视化

  可以看出明显存在两类数据，一类集中在左下角，一类集中在右上方。

构建感知器模型

  模拟一般python包的结构，这里我们自定义的一个类Percepter包含四个函数：

  • 构造函数
  • fit：通过误差反向传播训练模型。
  • net_input：计算输入到感知器的值
  • predict：接受输入数据，预测结果。

  构造函数主要是确定学习速率$\eta$和训练迭代次数n_iter。

  fit函数：首先初始化$W$为0，也可以是较小的随机数。这里注意，我们将阈值$\theta$作为$W$的一个分量来一起运算，因为$\theta$和$W$的更新公式中$\Delta W(n)$是一样的，这样做在编码上更加简单。然后对每个样本进行学习，使用上面提到的更新公式进行更新。

  net_input函数：这里实际上就是做向量点乘，计算出输入到这个感知器的值。

  predict函数：这里实际上就是激活函数。因为实际上，我们需要在二维平面上找到一条直线去将数据点分为两类，所以这里就是找一条直线，所以如果$Z>0$，那么就认为该数据点在直线的上方，反之，则认为该数据点在直线的下方。这样就能够区分出两个类别。

  errors_变量用于保存每一轮迭代计算出来的总错误数，以衡量训练的效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# Definition of class Percepter
class Percepter(object):
    '''
    eta: learning rate
    n_iter: training times
    w_: weight vector
    errors_:
    '''
    def __init__(self, eta = 0.01, n_iter=10):
        self.eta = eta;
        self.n_iter = n_iter
        pass

    '''
    Input: training data, x is input, y is label
    X: shape[n_samples, n_features]

    X: [[1, 2, 3], [4, 5, 6]], n_samples = 2, n_features = 3
    y:[1, -1]
    '''
    def fit(self, X, y):
        # Initialize w_ to 0
        self.w_ = np.zeros(1 + X.shape[1]);
        self.errors_ = []

        for _ in range(self.n_iter):
            errors = 0
            '''
            X:[[1, 2, 3], [4, 5, 6]]
            y:[1, -1]
            zip(X, y) = [[1, 2, 3,  1], [4, 5, 6,  -1]]
            '''
            for xi, target in zip(X, y):
                update = self.eta * (target - self.predict(xi))
                self.w_[1:] += update * xi
                self.w_[0] += update
                errors += int(update != 0.0)
                pass
            self.errors_.append(errors)
            pass
        pass
    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]
        pass
    def predict(self, X):
        return np.where(self.net_input(X) >= 0.0, 1, -1)
        pass
    pass

训练模型

  完成了感知器模型的构建后，训练模型就很简单了，只需要调用fit函数即可。这里我们同时打印出【错误-训练次数】曲线。

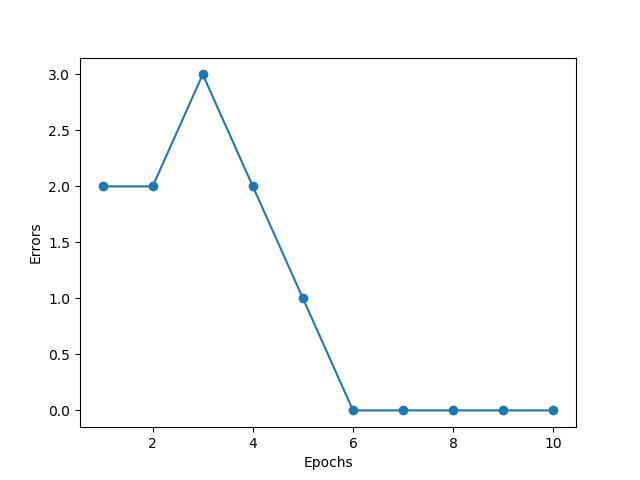
iris数据训练错误曲线

展示模型

  下面我们展示一下模型对于训练数据的分类情况。

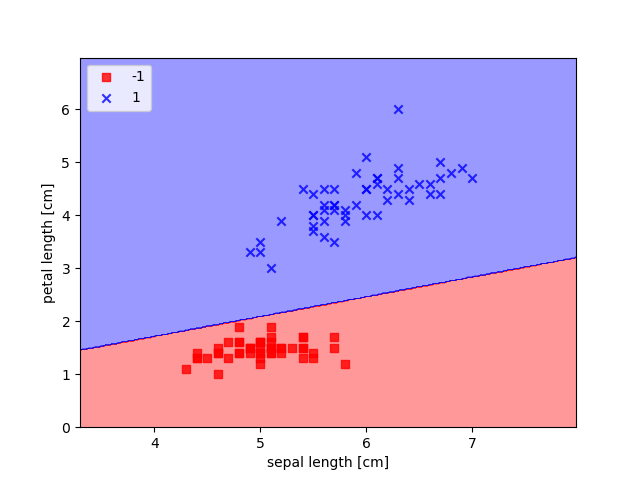
iris数据分类结果

  可以看出，数据被明显地分成了两类，也就是说对于训练集，模型的训练误差为0。也就是说，在给定的这么多数据的情况下，模型的训练已经达到最优了。这个二维平面也可以称作该模型的决策面。

  同时我们输出$W$，$W[0]$是阈值，$W[1]$和$W[2]$分别对应两个输入的参数。如果我们把两个输入看作是决策平面的$x,y$。那么划分这个平面的直线就可以这样表示：
$$
W[1]*x+W[2]*y+\theta=0
$$
  我们输出$W$是：

iris数据训练权重

  所以可以计算出该直线为：
$$
-0.68x+1.82y-0.4=0 \
y=0.37x+0.22
$$
  结合图像观察可以知道这是正确的。这也说明单个感知器做二维平面的分类实质上就是找到这样一条划分的直线。

总结

  以上就是感知器的原理和简单实现。单个感知器的功能已经是很强大，可以完成单独的一些分类任务，当然，如果将众多感知器结合起来，就构成了功能更加强大的神经网络。本篇博客的介绍就到这里，谢谢您的支持！

Welcome to my other publishing channels