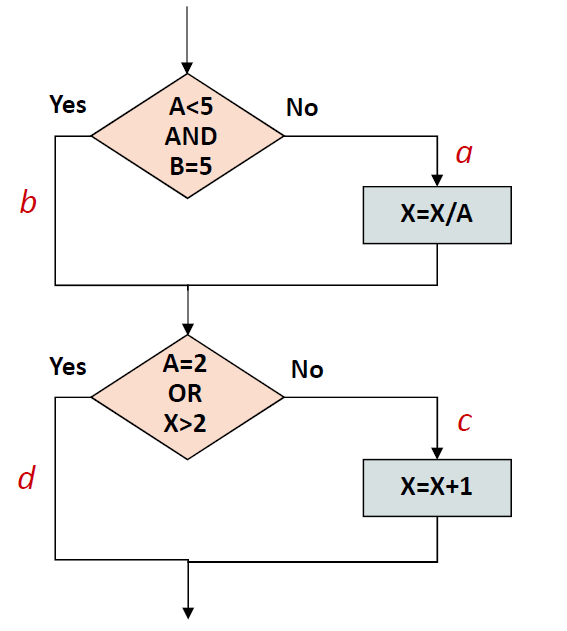
软件测试作业5
- 根据给出的程序流程图,完成:
- 画出相应的程序控制流图
- 给出控制流图的邻接矩阵
- 计算McCabe环形复杂度
- 找出程序的一个独立路径集合
Answer
基本路径测试的设计步骤
第一步:画出控制流图
程序流程图用来描述程序控制结构。将程序流程图映射到一个相应的**程序控制流图**。
控制流图中的圆称为流图的结点,代表一个或多个语句。流程图一个处理方框序列或一个菱形判决框都可被映射为流图的一个结点(简化起见假设程序流程图的菱形判决框不包含复合条件)。
流图中的箭头称为边或连接,代表控制流向。流图中的一条边必须终止于一个结点。由边和结点限定的封闭范围称为区域。计算区域时应包括外部域。
第二步:计算MaCabe环路复杂度
MaCabe环路复杂度为程序逻辑复杂性提供定量测度。该度量用于计算程序的基本独立路径数目,也即是确保所有语句至少执行一次的起码测试数量。
有以下三种方法计算环路复杂度:
- 给定流图$G$的环路复杂度$V(G)$,定义为$V(G) = m - n + 2$,$m$是流图中边的数量,$n$是流图中结点的数量;
- 平面流图中区域的数量对应于环路复杂度;
- 给定流图$G$的环路复杂度$V(G)$,定义为$V(G)=d+1$,$d$是流图$G$中单判定节点的数量。
第三步:准备测试用例
根据MaCabe环路复杂度的计算结果,可得知独立路径的数量。(一条独立路径是指,和其他的独立路径相比,至少引入一个新处理语句或一个新判断的程序通路。$V(G)$值正好等于该程序的独立路径的条数)
设计用例数据输入,确保基本路径集合中的每一条路径都得到执行。
第四步:应用测试用例
应用上一步设计的测试用例,结合预期结果进行结果分析。
作业答案
画出相应的程序控制流图。
首先将流程图转换为带标记的流程图,其中的标号代表运算式。得到:
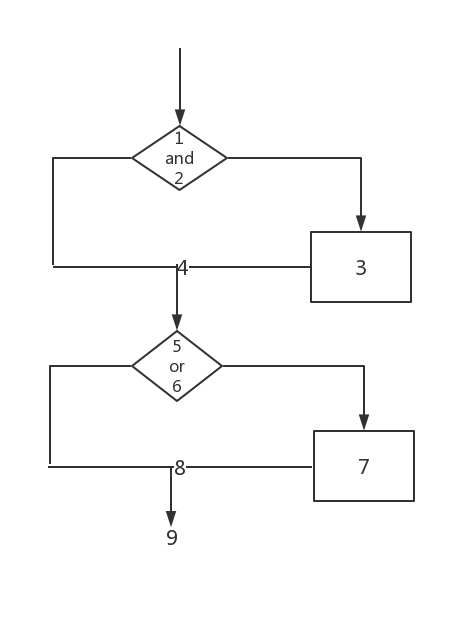
然后根据上面这个带标记的程序流程图,写出程序控制流图:
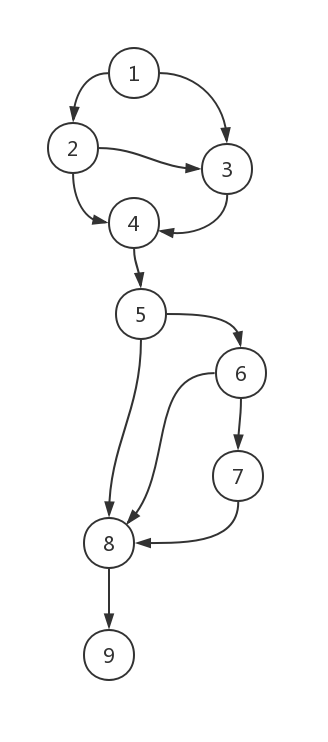
给出控制流图的邻接矩阵
$$
\left[
\begin{matrix}
0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0\
0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \
0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \
\end{matrix}
\right]
$$计算McCabe环形复杂度
给定流图$G$的环路复杂度$V(G)$,定义为$V(G) = m - n + 2$,$m$是流图中边的数量,$n$是流图中结点的数量;
$V(G) = 12 - 9 + 2 = 5$
平面流图中区域的数量对应于环路复杂度;
$V(G)=区域数 = 5$
给定流图$G$的环路复杂度$V(G)$,定义为$V(G)=d+1$,$d$是流图$G$中单判定节点的数量。
$v(G) = 4 + 1 = 5$
找出程序的一个独立路径集合
- 路径1:1$\rightarrow$2$\rightarrow$4$\rightarrow$5$\rightarrow$6$\rightarrow$7$\rightarrow$8$\rightarrow$9
- 路径2:1$\rightarrow$2$\rightarrow$4$\rightarrow$5$\rightarrow$6$\rightarrow$8$\rightarrow$9
- 路径3:1$\rightarrow$2$\rightarrow$4$\rightarrow$5$\rightarrow$8$\rightarrow$9
- 路径4:1$\rightarrow$2$\rightarrow$3$\rightarrow$4$\rightarrow$5$\rightarrow$8$\rightarrow$9
- 路径5:1$\rightarrow$3$\rightarrow$4$\rightarrow$5$\rightarrow$8$\rightarrow$9

