介绍
在日常生活的很多测试中,我们得到的数据都是由不同频率不同振幅的波形叠加起来的数据。在计算的时候需要逼近这种波形,选取具有周期性的三角函数作为基函数是合适的。对于计算傅里叶逼近系数问题,都可以统一地归结为:
$$
c_j = \sum^{N-1}_{k=0}x_k\omega^{kj}_N,j=0,1,\dots,N-1
$$,这就是N点DFT
其中${x_k}^{N-1}_0$为已知的输入数据点(采样点),${c_j}^{N-1}_0为输出数据$。
分析
为了减少乘法的次数,这里充分利用了三角函数的周期性。对于$\omega_N^{jk}(j,k=0,1,\dots,N-1)$而言,最多有N个不同的值。特别地,有
$$
\omega^0_N = \omega_N^N = 1, \omega_N^{N/2} = -1
$$
因此当$N = 2^p$时,$\omega_N^{jk}$只有$n/2$个不同的值,所以可以利用这个性质,将求和的式子分为两部分:
$$
c_j = \sum^{N/2-1}{k=0}x_k\omega_N^{jk} + \sum^{N/2-1}{k=0}x_{N/2+k}\omega^{j(N/2+k)}N = \sum^{N/2-1}{k=0}[x_k+(-1)^jx_{N/2+k}]\omega_{N}^{jk}
$$
分别奇数项和偶数项进行考察,得到:
$$
c_{2j} = \sum^{N/2-1}{k=0}(x_k + x_{N/2+k})\omega^{jk}{N/2},\
c_{2j+1} = \sum^{N/2-1}{k=0}(x_k - x_{N/2+k})\omega^k_N\omega^{jk}_{N/2}
$$
这样对每个点反复进行二分就可以得到FFT算法了。
实际计算的时候,为了减少运算量,可以将$k,j$用二进制表示,则
$$
c_j = c(j_2j_1j_0), x_k = x(k_2k_1k_0),
$$
引入如下记号简化算式:
$$
A_0(k_2k_1k_9) = x(k_2k_1k_0), \
A_1(k_1k_0j_0) = \sum^1_{k_2=0}A_0(k_2k_1k_0)\omega^{j_0(k_2k_1k_0)}, \
A_2(k_0k_1j_0) = \sum^1_{k_1=0}A_1(k_1k_0j_0)\omega^{j_1(k_1k_00)}, \
A_3(j_2j_1j_0) = \sum^1{k_0=0}A_2(k_0j_1j_0)\omega^{j_2(k_000)},
$$
如此类推,从$A_0(k)=x_k$一直计算到$A_p(j) = c_j$,就可以得出所有的A,这就是要求的系数。
代码实现
根据迭代公式
$$
\begin{cases}
A_q(k2^q+j) = A_{q-1}(k2^{q-1} + j) + A_{q-1}(k2^{q-1} + j + 2^{p-1})\
A_q(k2^q + j + 2^{q-1}) = [A_{q-1}(k2^{q-1} + j) - A_{q-1}(k2^{q-1} + j + 2^{p-1})]\omega^{k2^{q-1}}\
\end{cases}
$$
编写matlab代码。
1 | function [c] = FFT(A) |
在编写代码的过程中,特别需要注意要使用一个临时变量储存$A(q-1)$,因为在$j,k$循环的过程中,会不断更新$A(p)$,而$A(p)$的计算是基于$A(p-1)的$。
小结
运行上述代码后,我写了一个混杂了多种波形的信号进行变换,分析如下: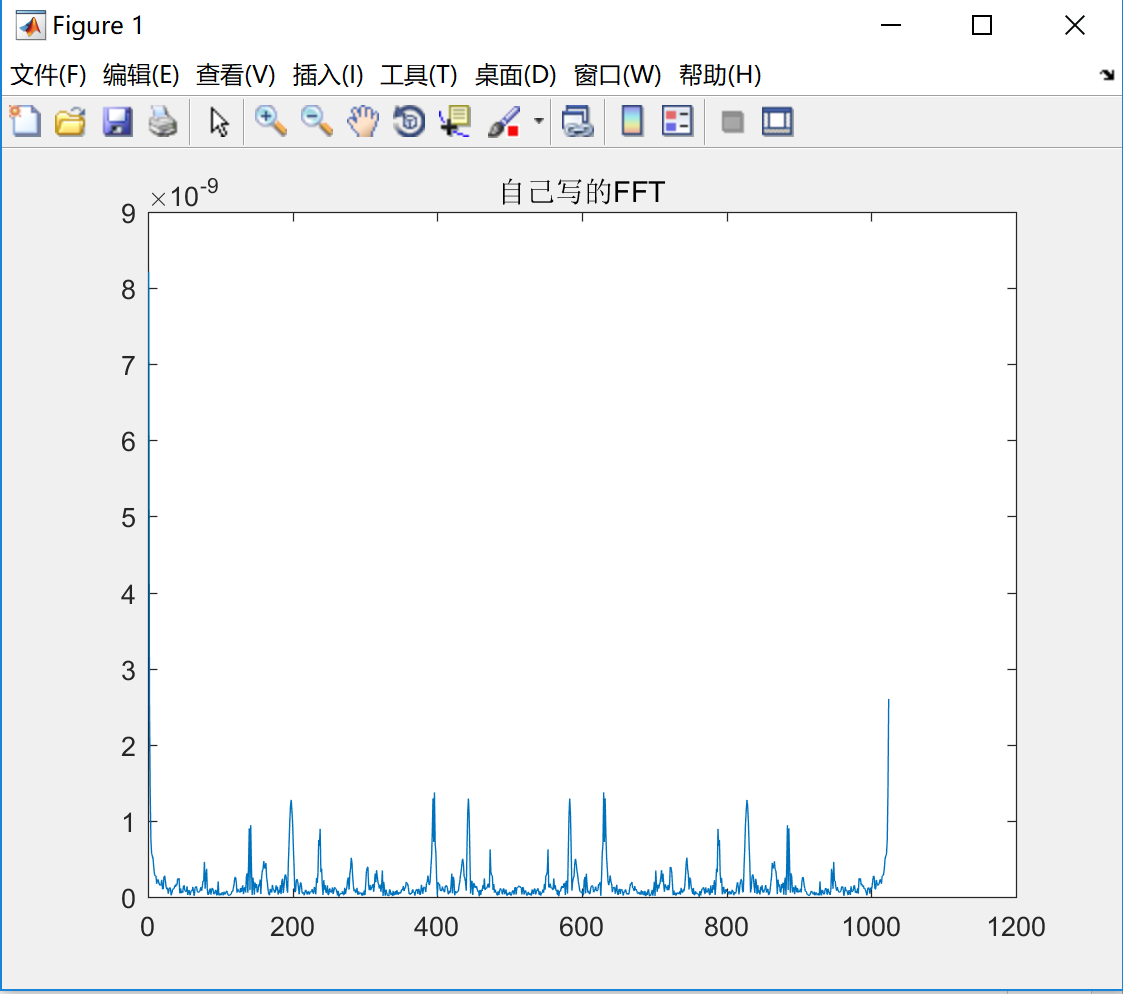
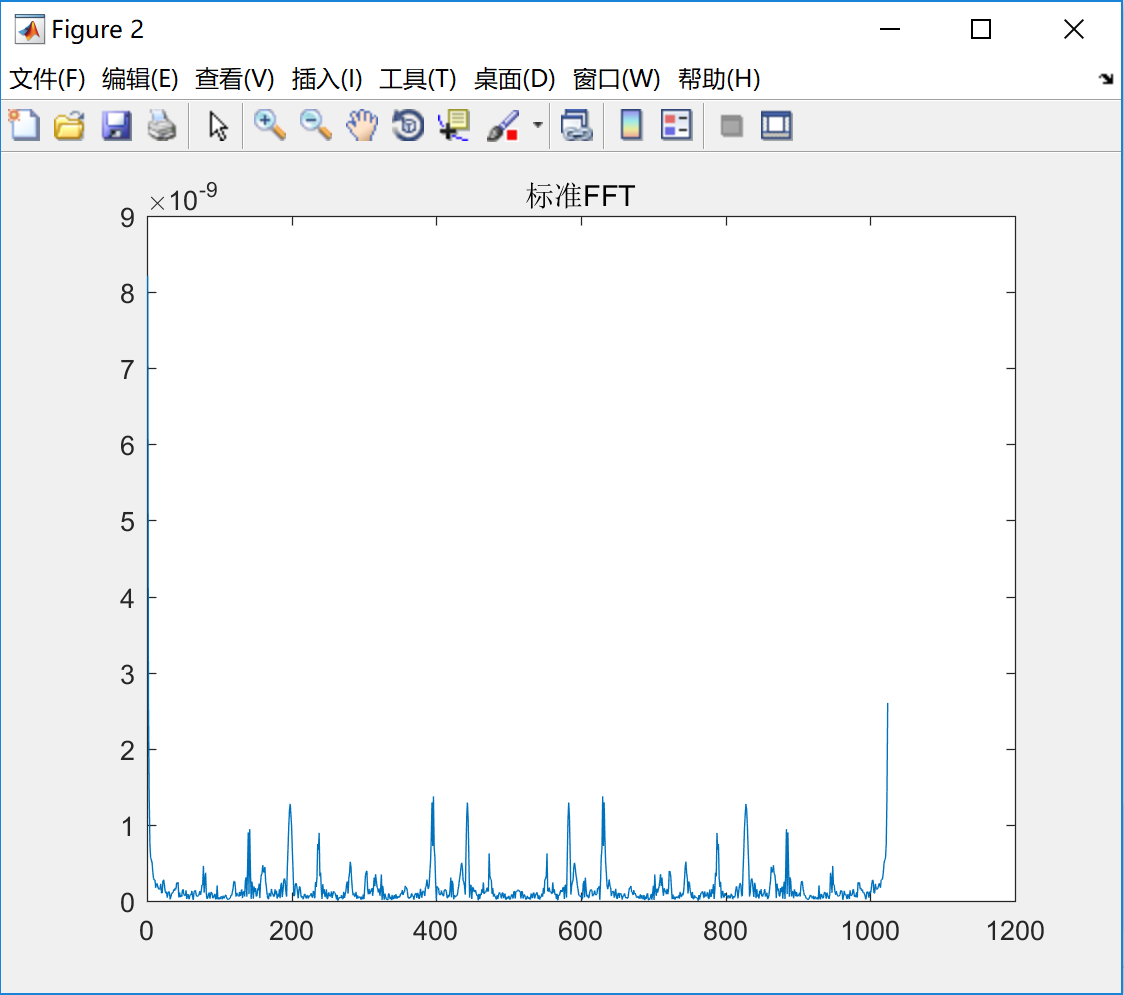
分析:上面的图是经过自己写的FFT算法得出的系数,下面的图是使用matlab自带的FFT方法求出的系数,对比两幅图基本一致,可以基本判断FFT算法实现正确。
傅里叶变换在数值分析中是一个相当重要的知识点,这里只是讲述了一些基本的思路和实现方法,并没有作深入的分析,日后我了解更多之后再详细分析,谢谢!
参考资料:
1.数值分析(第5版) 李庆扬,王能超,易大义 编

