递推最小二乘法

介绍

  我们在以前可能会在直线拟合的时候使用过最小二乘法，常用于处理实现数据，为了获得一条直线或者曲线。而在这里我们对更一般的情况做讨论。
  对于给定的超定线性方程组$Ax = b$，直接通过矩阵求解是困难的。这里就用到了逼近的思想。假设上述方程存在一个噪声$e$，则可以写成$b-Ax = e$，接下来要做的就是求解出能够极小化这个噪声的$x$。这就是递推最小二乘法需要解决的问题。

分析

  递推最小二乘法的思路是基于最小二乘法，采用递推的形式来求得最终的$x$。首先来分析$x$的形式：
$$
x^* = \min_x ||b-Ax||^2，
$$
对上述等式右边求一阶梯度：
$$
2A^T(Ax - b) = 0 \
x = (A^TA)^{-1}A^Tb
$$
得到了x的表示形式后，就可以根据每个$b(m)$来推导$x(m)$。
它的递推公式为：
$$
K(m) = \frac{P(m-1)\phi_m}{1+\phi_m^TP(m-1)\phi_m} \
P(m) = (I-K(m)\phi_m^T)P(m-1) \
\hat x(m) = \hat x(m-1) + K(m)(b_m - \phi_m^T\hat x(m-1))
$$
，其中$\phi_m^T$为矩阵$A$的第$m$行。
  每一步迭代，我们都通过在旧的估计值上，加上经过预测误差的真正测量值来得到新的估计值，最后得到较为准确的结果$x$。

代码实现

  根据上述推导的公式，编写matlab代码，特别需要注意$\phi_m^T$是$A(m,:)$，而$\phi_m$是$A(m,:)’$。

% 递推最小二乘法
function [result, error, count] = LeastSquares(A,b)
    m = 10000;
    n = 10;
    count = [];
    standard = lsqnonneg(A,b); % 标准答案
    p = 1000*eye(n); % p为n*n的单位矩阵
    x = zeros(n,1); % x为n*1的向量
    k = zeros(n,1); % k为n*1的向量;

    for i=1:m
        k = (p*A(i,:)') / (1 + A(i,:)*p*A(i,:)');
        p = (eye(n) - k*A(i,:)) * p;
        x = x + k * (b(i,1) - A(i,:)*x);
        error(i) = norm((x - standard),2);
        count(i) = i;
    end
    result = x;
end

小结

  实现并运行上述代码，进行简单的数值测试。
迭代步数-收敛精度曲线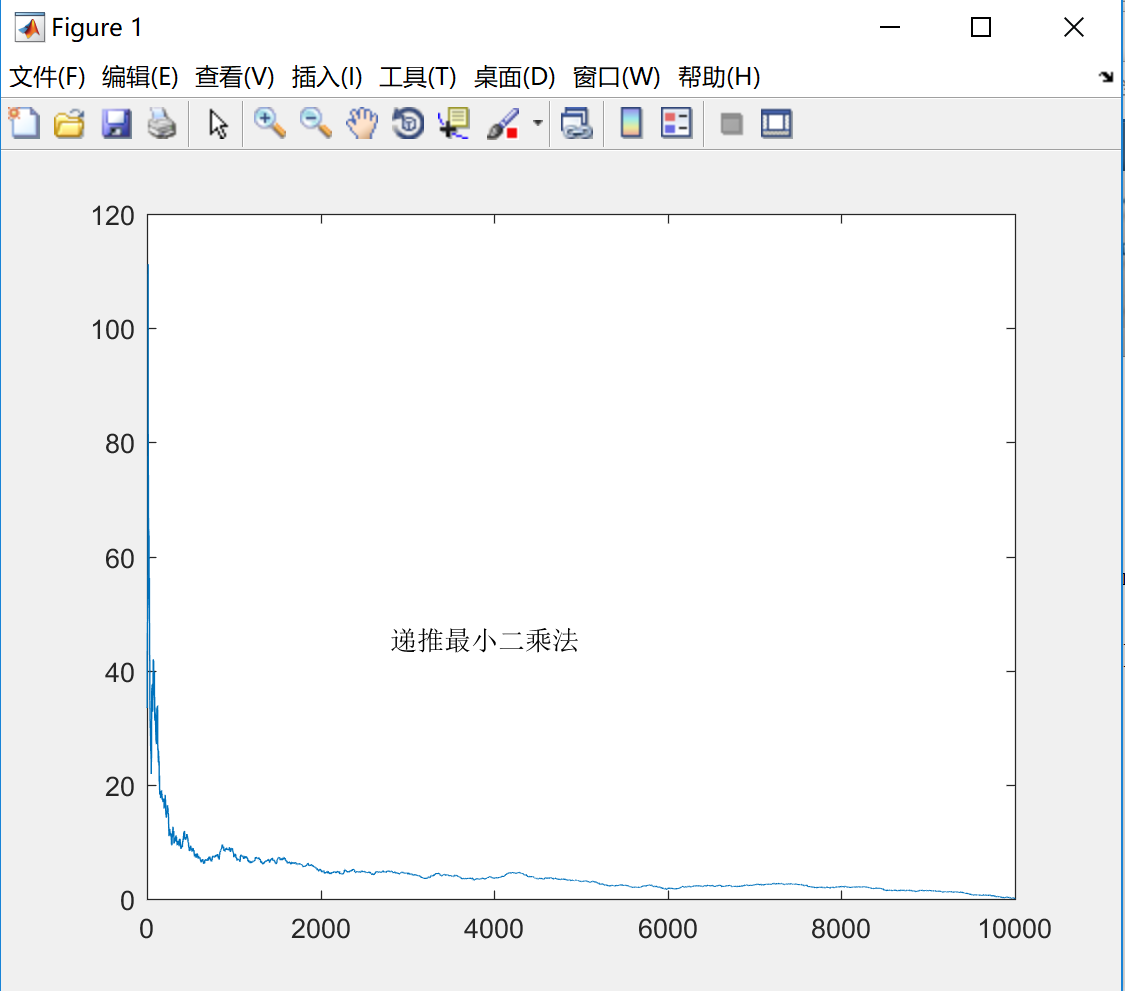

分析：从图中可以看出，递推最小二乘法最终也是可以求得一个精确解的。递推最小二乘法最大的特点是在线识别，需要存储的信息较少。但是如果给出的数据较少或者初值点比较粗糙，递推最小二乘法的精度会有所降低。
  递推最小二乘法的分析与实现就到这里了，谢谢！

---

参考资料：

1.数值分析（第5版） 李庆扬，王能超，易大义 编