Halo

A magic place for coding

0%

非线性方程求解之简化牛顿法

Posted on Edited on Valine:

介绍

  在前面我们提到了牛顿法求解非线性方程，但是牛顿法有一个明显的缺点，就是在每一步迭代中都要计算函数值和一阶导数，这个计算量是巨大而且困难的，因此我们希望减少这个计算，对牛顿法进行了改进–简化牛顿法。

分析

  简化牛顿法是牛顿法的变种，原因在于，牛顿法中每一步都需要计算$f(x_k)$和$f^{‘}(x_k)$，这是需要很大计算量的。除此之外，牛顿法中的初始近似$x_0$只在精确解$x^*$附近才能保证收敛。简化牛顿法就是为了解决这个问题的。首先给出简化牛顿法的迭代公式：
$$
x_{k+1} = x_k - Cf(x_k),
$$
则迭代函数为：$\phi(x) = x - Cf(x)$.
  若$|\phi^{‘}(x)| = |1-Cf^{‘}(x)| < 1$，即取$0 < Cf^{‘}(x) < 2$在根附近成立，则该迭代法局部收敛。
  同时取$C = \frac{1}{f^{‘}(x_0)}$，这样就只需要在第一步计算$f^{‘}(x_0)$，大大减少了计算量。其几何意义是用斜率为$f^{‘}(x_0)$的平行弦与$x$轴交点作为$x^*$的近似解。

代码实现

Matlab代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
% 简化牛顿法
function [y, count, error, time] = Newton1(x0, e)
    % y为最终结果
    % x为开始迭代的初始坐标
    % e为迭代精度
    k = 0; % 迭代次数变量
    err = 0;% 误差变量
    count = [];% 输出迭代次数的数组
    time = []; % 输出迭代时间的数组
    error = [];% 输出误差的数组
    n = 50; % n为最大迭代次数
    del_x = 0.0000001; % 用于求函数导数值的极小量
    y_deriv = (myFun(x0+del_x) - myFun(x0)) / del_x; % x0点的导数值
    y = x0;
    x0 = y + 1000; % 保证迭代能开始

tic
while 1
    if (abs(y-x0) <= e)
        disp('满足迭代精度');
        break;
    elseif (k > n)
        disp('迭代次数超界');
        break;
    else
        x0 = y;
        if((myFun(x0+del_x) - myFun(x0)) == 0)
                disp('导数为0');
                break;
        else
            y = x0 - myFun(x0) / y_deriv; % 简化牛顿法
            k = k + 1; % 迭代次数加1
            count(k) = k;
            err = abs(y-x0)/y;
            error(k) = err;
        end
    end
end
toc

    % 均分时间间隔
    temp = toc / k;
    for i=1:k
        time(i) = i*temp;
    end

    disp('简化牛顿迭代结束');
end

function [y] = myFun(x)
y = x*x - 115;
end

  其中myFun是需要求解的非线性方程。

小结

  对上面编写的代码进行了简单的数值实验，结果如下：
迭代步数与误差的关系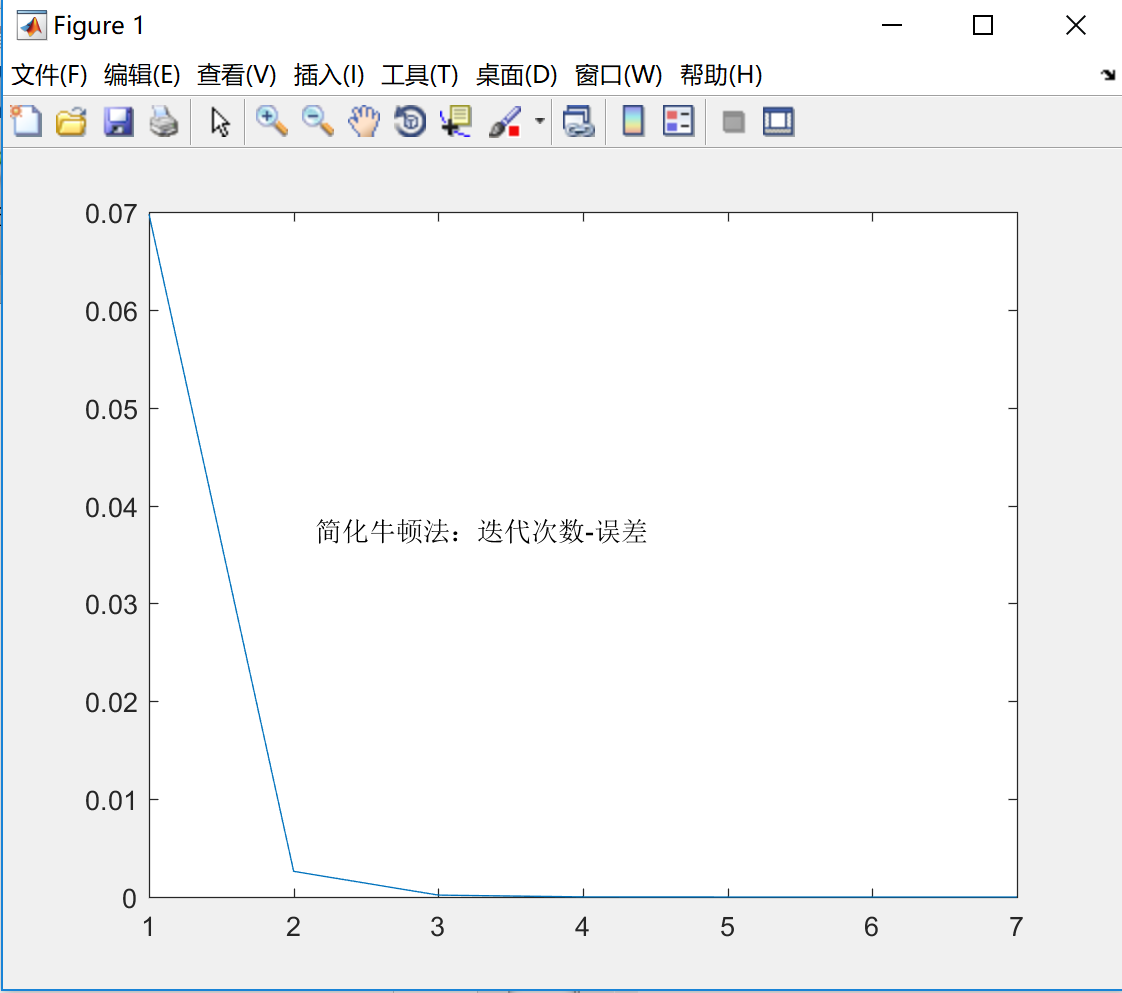
简化牛顿法结果1
计算时间与误差的关系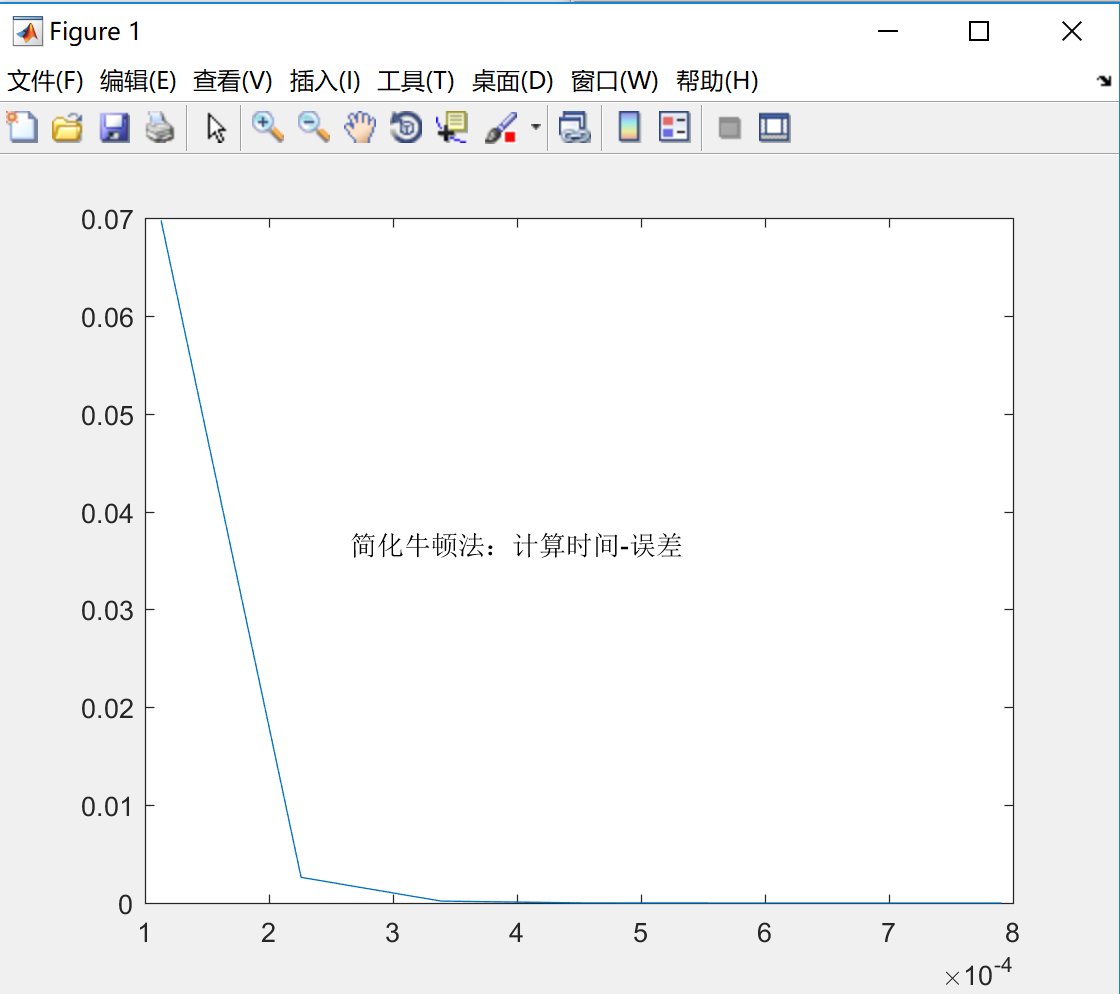
简化牛顿法结果2
分析：从结果分析，简化牛顿法的迭代次数要比牛顿法多，这说明简化牛顿法的收敛速度是不如牛顿法的。它的特点是减少了运算量，但是收敛速度是线性的。
 简化牛顿法比牛顿法更有应用价值，对简化牛顿法的分析和讲解就到这里了，谢谢！

参考资料：

1.数值分析（第5版） 李庆扬，王能超，易大义 编

Welcome to my other publishing channels