Halo

A magic place for coding

0%

非线性方程求解之弦截法

Posted on Edited on Valine:

介绍

  前面提到的简化牛顿法是对牛顿法的一个改进，今天我就来介绍另一个基于牛顿法改进的方法–弦截法。它主要是从插值的角度来对牛顿法进行改进。

分析

  弦截法也是牛顿法的一个变种，同样也是为了避免计算$f^{‘}(x_k)$。这里采用的方法是使用已求的函数值$f(x_k),f(x_{k-1}),…$来回避导数值$f^{‘}(x_k)$的计算，这种方法是建立在插值原理的基础上的。
  设$x_k, x_{k-1}$是$f(x) = 0$的近似根，我们利用$f(x_k),f(x_{k-1})$构造一次插值多项式$p_1(x)$，并用$p_1(x) = 0$的根作为$f(x) = 0$的新的近似根$x_{k+1}$，根据一次插值公式：
$$
p_1(x) = f(x_k) + \frac{f(x_k) - f(x_{k-1})}{x_k - x_{k-1}}(x - x_k)，
$$
因此有
$$
x_{k+1} = x_k - \frac{f(x_k)}{f(x_k) - f(x_{k-1})}(x_k - x_{k-1})，
$$
以上就是弦截法的迭代公式了。与牛顿法对比，不难看出，弦截法使用$\frac{f(x_k) - f(x_{k-1})}{x_k - x_{k-1}}$代替了牛顿法中的导数$f^{‘}(x_k)$。
  弦截法的几何意义是，使用曲线$y = f(x)$上的两点$x_k, x_{k-1}$的弦线与$x$轴的交点作为作为$x^*$的近似解。弦截法与牛顿法都是线性化方法，但是两者有很大不同。牛顿法在计算$x_{k+1}$的时候只用到了上一步的结果$x_k$，而弦截法在求$x_{k+1}$时要用到前两部的计算结果$x_k$，$x_{k-1}$，因此在使用弦截法的时候要首先给出两个值$x_0$，$x_1$。

代码实现

Matlab代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
% 弦截法
function [y, count, error, time] = Secant(x0, x1, e)
    % y为最终结果
    % x为开始迭代的初始坐标
    % e为迭代精度
    n = 50; % n为最大迭代次数
    k = 0;% 迭代次数变量
    err = 0;% 误差变量
    count = [];%输出迭代次数的数组
    time = []; % 输出迭代时间的数组
    error = [];% 输出误差的数组

    tic
    while 1
        y = x1 - myFun(x1) * (x1 - x0) / (myFun(x1) - myFun(x0));
        err = abs(y - x1) / y;
        if (abs(y - x1) <= e)
            disp('满足迭代精度');
            break;
        elseif (k > n)
            disp('迭代次数超界');
            break;
        else
            x0 = x1;
            x1 = y;
            k = k + 1;
            count(k) = k;
            error(k) = err;
        end
    end
    toc

    % 均分时间间隔
    temp = toc / k;
    for i=1:k
        time(i) = i*temp;
    end

    disp('弦截法迭代结束');
end

function [y] = myFun(x)
y = x*x - 115;
end

小结

  对上述实现的代码进行简单的数值实验，结果如下：
迭代步数与误差的关系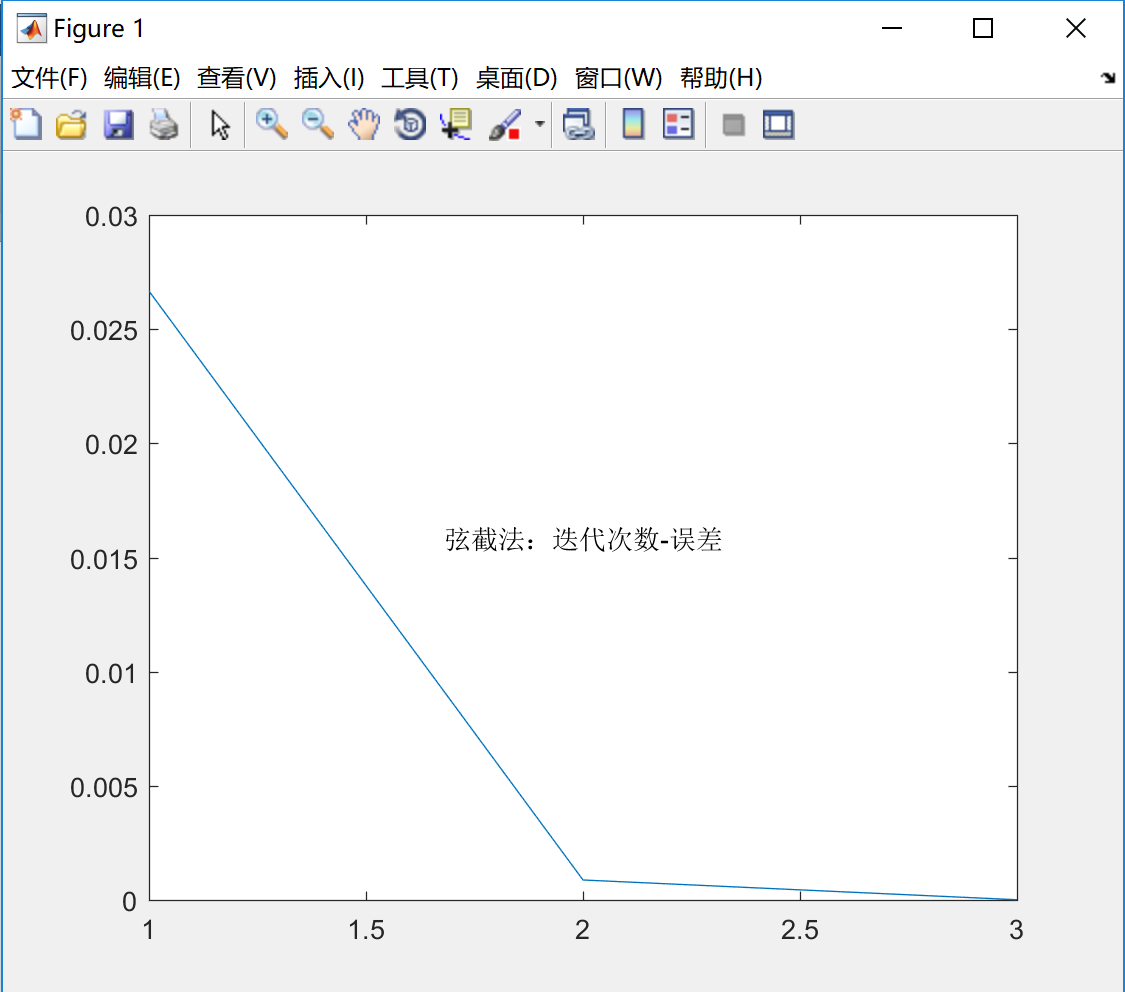
弦截法结果1
计算时间与误差的关系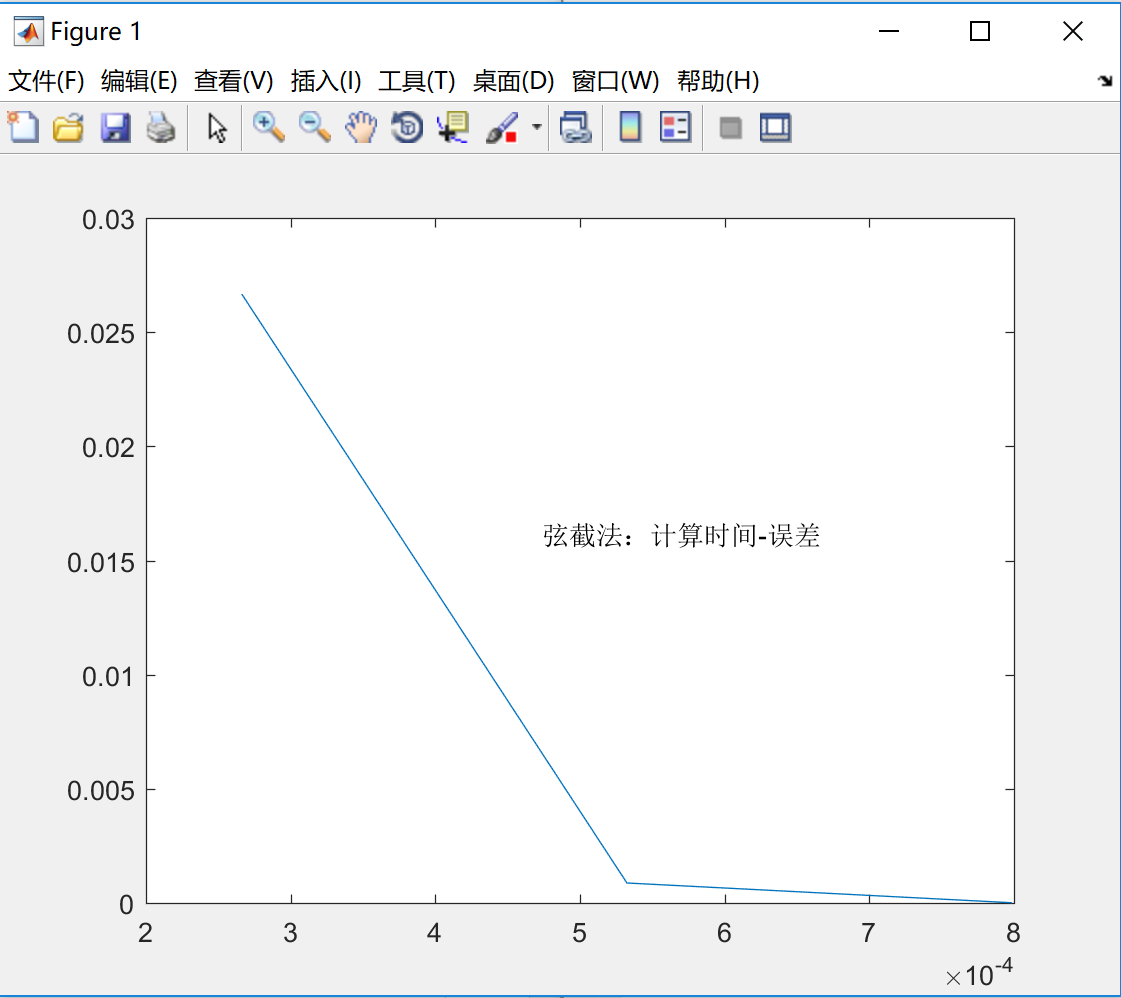
弦截法结果2
分析：由结果分析可知，弦截法的迭代次数和计算时间都是最少的。从理论上讲，牛顿法在精确解$x^*$附近是平方收敛的，而弦截法是超线性收敛的，收敛速度约为1.618，但是在这里，由于我选取的前两个点是$x=10$和$x=11$，非常接近精确解，所以迭代步数会比牛顿法要少。如果换成其他更加复杂和庞大的数据，牛顿法的收敛速度会比弦截法快。

  弦截法在计算下一步的值的时候需要用到前两步的结果，其收敛速度虽然没有达到牛顿法的平方收敛，但是也是相当快的。
  关于弦截法的分析与实现就到这里了，谢谢！

参考资料：

1.数值分析（第5版） 李庆扬，王能超，易大义 编

Welcome to my other publishing channels