LeetCode解题报告（208）-- 1217. Minimum Cost to Move Chips to The Same Position

Problem

We have n chips, where the position of the ith chip is position[i].

We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:

position[i] + 2 or position[i] - 2 with cost = 0.
position[i] + 1 or position[i] - 1 with cost = 1.

Return the minimum cost needed to move all the chips to the same position.

Example 1:

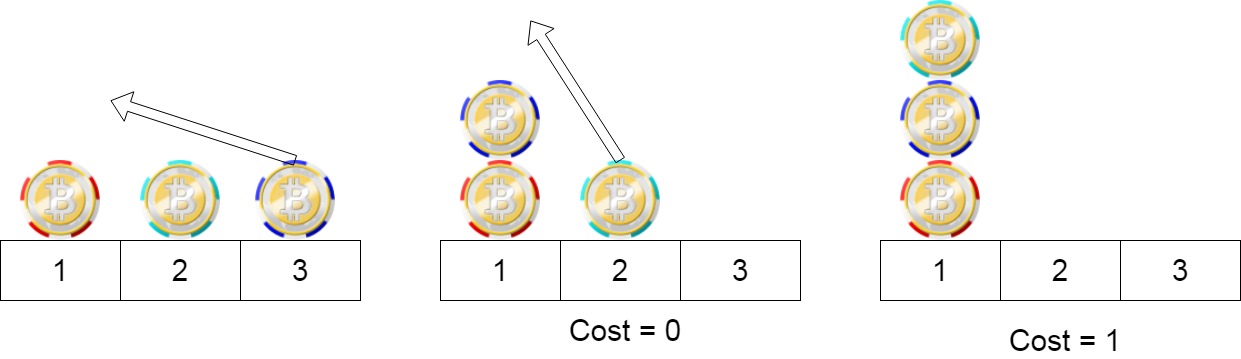
Input: position = [1,2,3]
Output: 1
Explanation: First step: Move the chip at position 3 to position 1 with cost = 0.
Second step: Move the chip at position 2 to position 1 with cost = 1.
Total cost is 1.

Example 2:

1
2
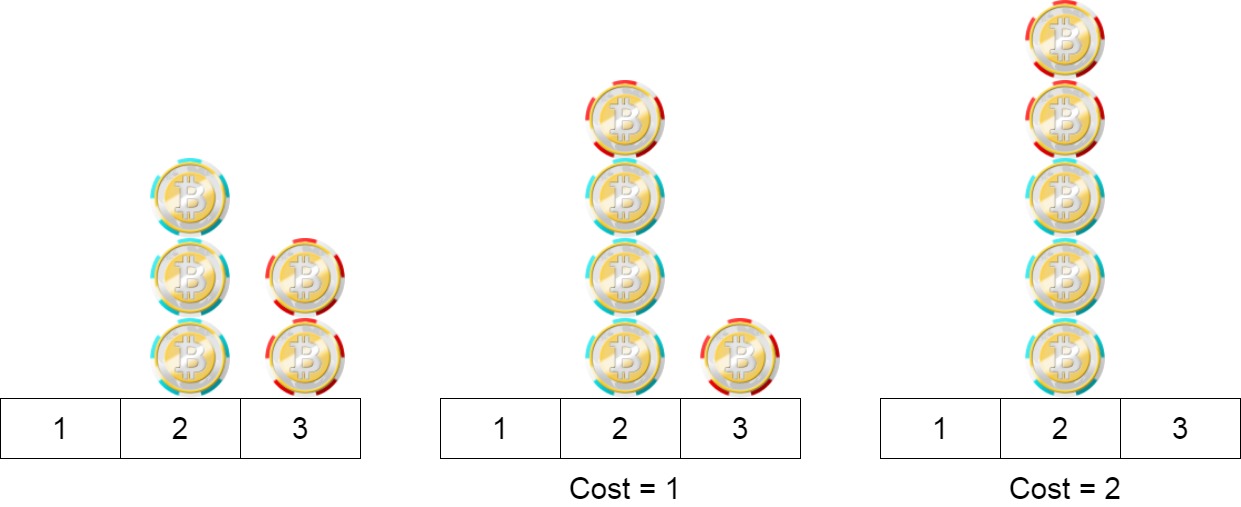
3

Input: position = [2,2,2,3,3]
Output: 2
Explanation: We can move the two chips at poistion 3 to position 2. Each move has cost = 1. The total cost = 2.

Example 3:

1 2	Input: position = [1,1000000000] Output: 1

Constraints:

1 <= position.length <= 100
1 <= position[i] <= 10^9

Analysis

这道题目是非常典型的操作类题目。之前的题解中我也有提到过解决这类问题的方法，要优先考虑巧解，因为如果一步一步操作的话，往往会有超时的问题。我们先来看题目的背景：chip散落在不同的位置，移动偶数个位置是不需要花费cost；移动奇数个位置就需要消费，每动一次花费一个cost。

其实这个题目的条件背后隐藏着一个规律，就是chip从一个位置到另一个位置，要么不用花费cost（偶数个位置不需要花费），要么花费1（奇数个位置可以先移动偶数个位置，最后一个移动一下就可以）。所以题目虽然说最后所有的chip要移动到同一个位置，实际上都是奇数位置的相当于是同一个位置，偶数位置也相当于同一个位置，所以答案也就呼之欲出了：占少数位置的移动到占多数位置的。

Solution

确定思路之后，这道题目的coding非常简单了，统计一奇数位置的个数，然后占少数的移动，每个chip都花费一个cost，最后计算出总数即可。

Code

class Solution {
public:
    int minCostToMoveChips(vector<int>& position) {
        int size = position.size();
        
        int oddCount = 0;
        for (int i = 0; i < size; i++) {
            if (position[i] % 2) {
                oddCount++;
            }
        }
        return min(oddCount, size - oddCount);
    }
};

Summary

这类题目一般都需要巧解，面对这类型的题目第一时间不是去考虑算法，而是找到突破口，题目给出的几个example也算是比较有代表性，尤其是example3有很强的指导性，相信这类题目碰见几次之后就会有感觉了。这道题目的分享到这里，谢谢！