LeetCode解题报告（293)-- 1091. Shortest Path in Binary Matrix

Problem

In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

• Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
• C_1 is at location (0, 0) (ie. has value grid[0][0])
• C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
• If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).

Return the length of the shortest such clear path from top-left to bottom-right. If such a path does not exist, return -1.

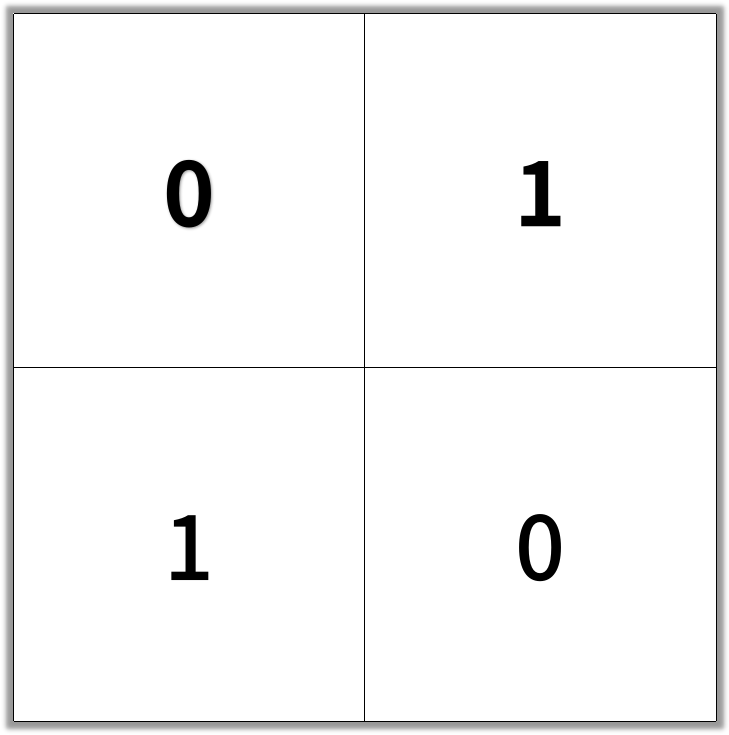
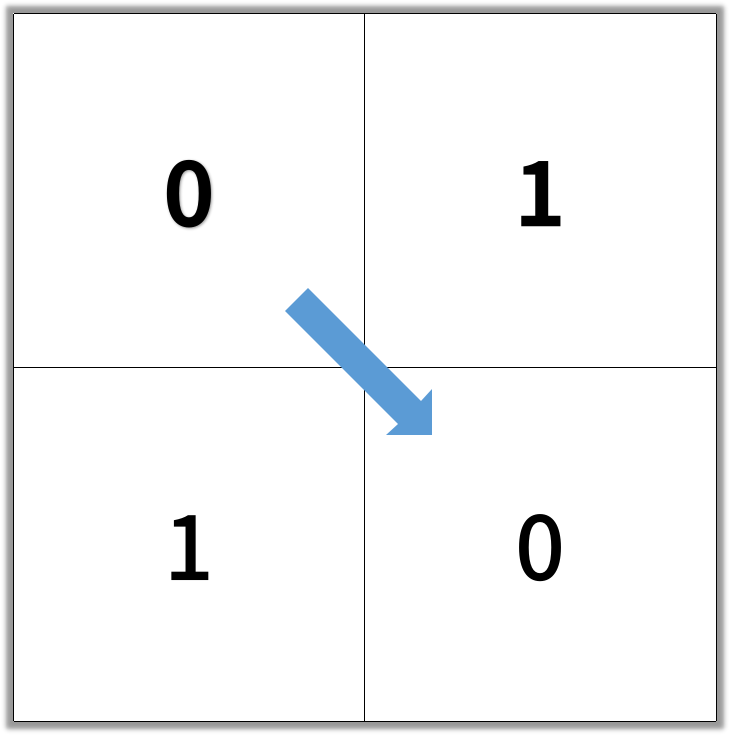
Example 1:

Input: [[0,1],[1,0]]
Output: 2

Example 2:

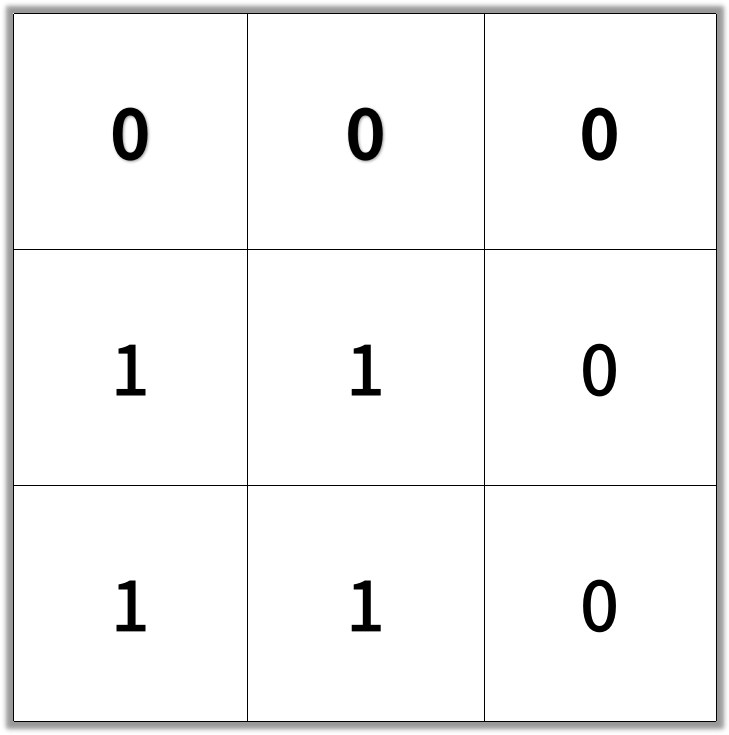
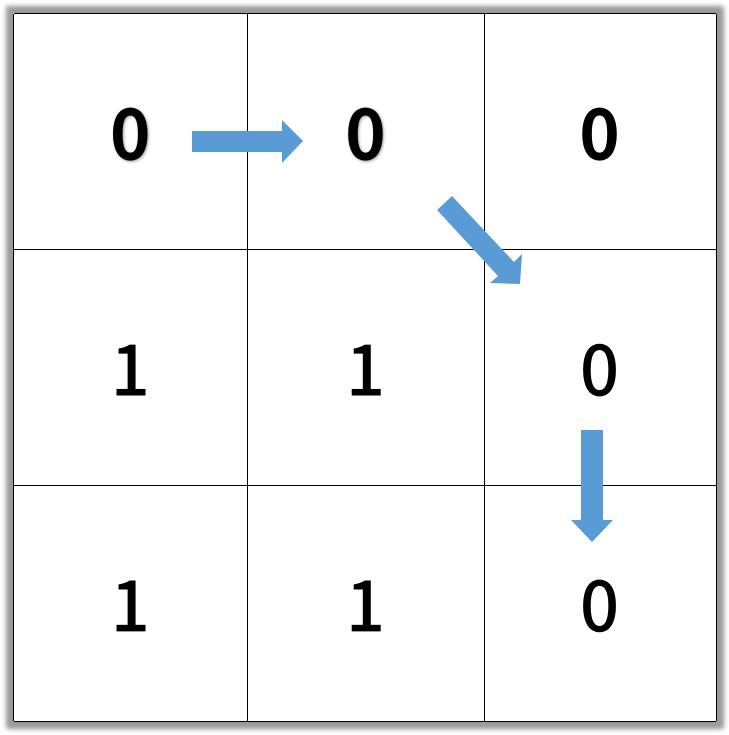
Input: [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Note:

1. 1 <= grid.length == grid[0].length <= 100
2. grid[r][c] is 0 or 1

---

Analysis

  这道题目是一道很常规的图BFS题目，要求找出最短的路径。可以走的路径是为0的位置，每个位置可以往周围8个方向进行行走。按照常规的图BFS做即可，主要有几个点：

1. 需要要有个visited矩阵去记录走过了哪些位置；
2. 有一个数组帮助我们向8个方向计算坐标。

  因为我们是用BFS，所以不需要维护最小值，第一个走到终点的就是最优解。

---

Solution

  特别注意当起点为1的时候，直接return -1。

---

Code

class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        
        vector<vector<int>> visited(m, vector<int>(n, 0));
        queue<pair<int, int>> q;
        if (grid[0][0] == 1) {
            return -1;
        }
        q.push({0, 0});
        
        int result = 0;
        while (!q.empty()) {
            int size =  q.size();
            result++;
            for (int i = 0; i < size; i++) {
                auto [x, y] = q.front();
                q.pop();
                if (x == m - 1 && y == n - 1) {
                    return result;
                }
                
                for (int k = 0; k < 8; k++) {
                    int dx = x + dirs[k][0];
                    int dy = y + dirs[k][1];
                    if (dx < 0 || dx == m || dy < 0 || dy == n) {
                        continue;
                    }
                    if (visited[dx][dy]++ || grid[dx][dy]) {
                        continue;
                    }
                    q.emplace(dx, dy);
                }
            }
        }
        return -1;
    }
private:
    int dirs [8][2] = {{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}};
};

---

Summary

  这道题目是图的BFS的基础题目，是其他图题目的基础。这道题目的分享到这里，谢谢您的支持！