LeetCode解题报告（294)-- 785. Is Graph Bipartite?

Problem

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

There are no self-edges (graph[u] does not contain u).
There are no parallel edges (graph[u] does not contain duplicate values).
If v is in graph[u], then u is in graph[v] (the graph is undirected).
The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example 1:

1
2
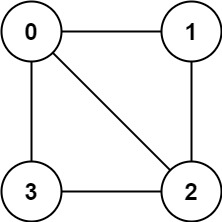
3

Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

1
2
3

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:

graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] does not contain u.
All the values of graph[u] are unique.
If graph[u] contains v, then graph[v] contains u.

Analysis

这是一道有关二分图的题目，好像是第一次遇到。简单来说，题目给了一个图，要求判断这个图是否是二分图。这里我们使用染色法，我们把同一条边的两个节点染成不同的颜色（使用1和-1表示），每个节点只能有一种颜色，如果一个节点需要染成两种不同的颜色，就说明这个图没有办法二分。我们对每个节点都这样做，分类处理：

如果该节点没有被染色，染色成1或-1。染成什么颜色是根据这条边上另一个节点的颜色决定的。第一个节点默认染成1；
如果该节点被染色，判断当前的颜色和该染的颜色是否一致，如果不一致说明有冲突，直接return false；如果一致，说明当前这个节点处理成功，然后把它相关的边都处理一遍。

Solution

我们需要一个数组去记录每个节点染的颜色，默认值0是没有染色。对于染色来说，如果一条边上其中一个节点的颜色是1，那么另一个节点就需要染成-1，这里我们直接乘上一个-1就行。

Code

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int size = graph.size();
        vector<int> colors(size, 0);
        for (int i = 0; i < size; i++) {
            if (colors[i] == 0 && !helper(graph, 1, i, colors)) {
                return false;
            }
        }
        return true;
    }
private:
    bool helper(vector<vector<int>>& graph, int color, int current, vector<int>& colors) {
        if (colors[current] != 0) {
            return colors[current] == color;
        }
        colors[current] = color;
        for (int i: graph[current]) {
            if (!helper(graph, -1 * color, i, colors)) {
                return false;
            }
        }
        return true;
    }
};

Summary

这道题目是二分图的题目，本质是对节点的染色，并没有涉及到图的遍历。这道题目的分享到这里，谢谢您的支持！