Halo

A magic place for coding

0%

LeetCode解题报告（445）-- 1548. The Most Similar Path in a Graph

Posted on Edited on Valine:

Problem

We have n cities and m bi-directional roads where roads[i] = [ai, bi] connects city ai with city bi. Each city has a name consisting of exactly three upper-case English letters given in the string array names. Starting at any city x, you can reach any city y where y != x (i.e., the cities and the roads are forming an undirected connected graph).

You will be given a string array targetPath. You should find a path in the graph of the same length and with the minimum edit distance to targetPath.

You need to return the order of the nodes in the path with the minimum edit distance. The path should be of the same length of targetPath and should be valid (i.e., there should be a direct road between ans[i] and ans[i + 1]). If there are multiple answers return any one of them.

The edit distance is defined as follows:

edit distance

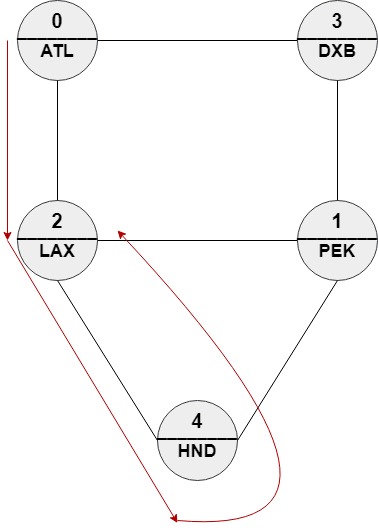
Example 1:

Example1

1
2
3
4
5
6
Input: n = 5, roads = [[0,2],[0,3],[1,2],[1,3],[1,4],[2,4]], names = ["ATL","PEK","LAX","DXB","HND"], targetPath = ["ATL","DXB","HND","LAX"]
Output: [0,2,4,2]
Explanation: [0,2,4,2], [0,3,0,2] and [0,3,1,2] are accepted answers.
[0,2,4,2] is equivalent to ["ATL","LAX","HND","LAX"] which has edit distance = 1 with targetPath.
[0,3,0,2] is equivalent to ["ATL","DXB","ATL","LAX"] which has edit distance = 1 with targetPath.
[0,3,1,2] is equivalent to ["ATL","DXB","PEK","LAX"] which has edit distance = 1 with targetPath.

Example 2:

Example2

1
2
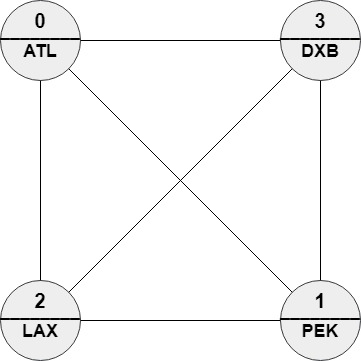
3
Input: n = 4, roads = [[1,0],[2,0],[3,0],[2,1],[3,1],[3,2]], names = ["ATL","PEK","LAX","DXB"], targetPath = ["ABC","DEF","GHI","JKL","MNO","PQR","STU","VWX"]
Output: [0,1,0,1,0,1,0,1]
Explanation: Any path in this graph has edit distance = 8 with targetPath.

Example 3:

Example3

1
2
3
4
Input: n = 6, roads = [[0,1],[1,2],[2,3],[3,4],[4,5]], names = ["ATL","PEK","LAX","ATL","DXB","HND"], targetPath = ["ATL","DXB","HND","DXB","ATL","LAX","PEK"]
Output: [3,4,5,4,3,2,1]
Explanation: [3,4,5,4,3,2,1] is the only path with edit distance = 0 with targetPath.
It's equivalent to ["ATL","DXB","HND","DXB","ATL","LAX","PEK"]

Constraints:

  • 2 <= n <= 100
  • m == roads.length
  • n - 1 <= m <= (n * (n - 1) / 2)
  • 0 <= ai, bi <= n - 1
  • ai != bi
  • The graph is guaranteed to be connected and each pair of nodes may have at most one direct road.
  • names.length == n
  • names[i].length == 3
  • names[i] consists of upper-case English letters.
  • There can be two cities with the same name.
  • 1 <= targetPath.length <= 100
  • targetPath[i].length == 3
  • targetPath[i] consists of upper-case English letters.

Analysis

  这道题目是把编辑距离应用到了一个图上面，题目定义图中一的一条路径的编辑距离，是该路径和题目给出的targetPath中不相同的节点的个数（两条路径长度是一样的）。因为这里有两条路径，一条是我要找的路径，另一条是题目给出的targetPath，然后题目要求的是最小的编辑距离，这两个信息提示有可能是dp，而且是二维dp。

  对二维dp状态的设计一般有一个原则，就是一个状态是属于第一条路径，一个状态是属于第二条路径。我定义dp[i][j]为在第i个城市并且是在targetPath中第j个位置的最小编辑距离。然后先来看base case，base case就是第1个位置（下标为0）和targetPath的第一个城市一样，就初始化为0，其余的为1（不一样就是1了）。

  然后我们来看转移方程，按照dp的套路，对所有的状态进行穷举，所以i的范围就是城市的数量n，j的范围就是[1, targetPath.size()]。如果targetPath[j]和i对应的城市一样的话，那么编辑距离就是0，否则就是1。然后怎么更新呢？对于dp[i][j]来说，它的上一个状态应该是dp[k][j - 1]，k是i所有的邻居，因为你不知道上一个最短的是哪个城市。因此需要把i的所有邻居都遍历一遍，找到最小的dp[k][j - 1]，然后加上上面的cost就是新的dp[i][j]。

  这道题目还没有结束，因为题目最后要求返回的不是最小的编辑距离，而是那条路径，这就涉及到了dp中如何找到真正的答案。其实原理并没有很复杂，就是再开一个同等大小的parent数组，记录好是从哪个状态转移到当前状态的。上面提到，dp[i][j]是从i的所有邻居中找最小的dp[k][j - 1]，那我们就记住这个k。计算完dp后，我们遍历一遍dp[i][size - 1]，找到最小的那个答案，然后以最小的那个i作为last，不断通过上面的记录的parent数组往前找，得到的结果就是路径。

Solution

  无。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution {
public:
    vector<int> mostSimilar(int n, vector<vector<int>>& roads, vector<string>& names, vector<string>& targetPath) {
        int size = targetPath.size();
        
        // build graph
        vector<vector<int>> graph(n);
        for (vector<int> &road: roads) {
            graph[road[0]].push_back(road[1]);
            graph[road[1]].push_back(road[0]);
        }
        
        vector<vector<int>> dp(n, vector<int>(size, INT_MAX));
        vector<vector<int>> parent(n, vector<int>(size, INT_MAX));
        
        // base case
        string start = targetPath[0];
        for (int i = 0; i < n; i++) {
            dp[i][0] = (names[i] == start) ? 0: 1;
        }
        
        for (int i = 1; i < size; ++i) {
            for (int j = 0; j < n; ++j) {
                string city = targetPath[i];
                int cost = names[j] == city ? 0: 1; // edit distance
                int minCost = INT_MAX;
                
                // loop all neighbors
                for (int &neighbor: graph[j]) {
                    if (dp[neighbor][i - 1] + cost < minCost) {
                        minCost = dp[neighbor][i - 1] + cost;
                        parent[j][i] = neighbor;
                    }
                }
                
                dp[j][i] = minCost;
            }
        }
        
        // get answer
        vector<int> result(size);
        
        int finalMinCost = INT_MAX;
        int last = -1;
        for (int i = 0; i < n; ++i) {
            if (dp[i][size - 1] < finalMinCost) {
                finalMinCost = dp[i][size - 1];
                last = i;
            }
        }
        
        for (int i = size - 1; i >= 0; i--) {
            result[i] = last;
            last = parent[last][i];
        }
        return result;
    }
};

Summary

  这道题目是一道非常综合的dp，基本上把dp的难点都包含在内。包括二维dp中，从上一个状态找出最小的转移到当前状态，以及如何通过parent数组记录状态转移，最终回溯出结果。这道题目的分享到这里，感谢你的支持！

Welcome to my other publishing channels