Halo

A magic place for coding

0%

LeetCode解题报告（446）-- 549. Binary Tree Longest Consecutive Sequence II

Posted on Edited on Valine:

Problem

Given the root of a binary tree, return the length of the longest consecutive path in the tree.

A consecutive path is a path where the values of the consecutive nodes in the path differ by one. This path can be either increasing or decreasing.

  • For example, [1,2,3,4] and [4,3,2,1] are both considered valid, but the path [1,2,4,3] is not valid.

On the other hand, the path can be in the child-Parent-child order, where not necessarily be parent-child order.

Example 1:

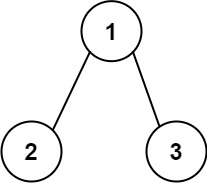
Example1

1
2
3
Input: root = [1,2,3]
Output: 2
Explanation: The longest consecutive path is [1, 2] or [2, 1].

Example 2:

Example2

1
2
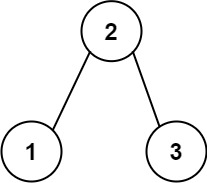
3
Input: root = [2,1,3]
Output: 3
Explanation: The longest consecutive path is [1, 2, 3] or [3, 2, 1].

Constraints:

  • The number of nodes in the tree is in the range [1, 3 * 104].
  • -3 * 104 <= Node.val <= 3 * 104

Analysis

  这是一道二叉树的题目，题目要求找出树中最长的连续路径，可以是递增的，也可以是递减。这里的路径指的是任意两个节点。先说一种很直接的方法，把树变成一副图，用一个map存储每个节点的父节点，然后做一遍BFS/DFS，找到最长的连续路径。但似乎这样就没有充分利用到了二叉树的特点，二叉树题目一般来说都可以通过递归来解决，那么这里我们能不能也用递归呢？

  答案当然是可以的。那我们需要在节点直接传递什么信息呢？对于父节点来说，如果它的左子树+它本身+它的右子树构成了一条连续的路径，那么长度应该是左子树路径的长度+右子树路径的长度+1。而我们这里又分递增和递减，因此每个节点应该返回两个值，一个是递增的路径长度，另一个是递减的路径长度。

  然后在处理节点时，比较root->val和root->left->val（如果存在），以及root->val和root->right->val（如果存在），去判断是否构成连续的路径，然后把对应的长度相加起来。需要注意，经过节点本身的最长路径应该是递增+递减，因为节点本身是一个中间点，然后维护一个最大值。

Solution

  无。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int longestConsecutive(TreeNode* root) {
        result = 0;
        helper(root);
        return result;
    }
private:
    int result;
    vector<int> helper(TreeNode* root) {
        if (!root) {
            return {0, 0};
        }
        
        int increase = 1, decrease = 1;
        if (root->left) {
            vector<int> left = helper(root->left);
            if (root->val == root->left->val + 1) {
                decrease = left[1] + 1;
            } else if (root->val == root->left->val - 1) {
                increase = left[0] + 1;
            }
        }
        
        if (root->right) {
            vector<int> right = helper(root->right);
            if (root->val == root->right->val + 1) {
                decrease = max(decrease, right[1] + 1);
            } else if (root->val == root->right->val - 1) {
                increase = max(increase, right[0] + 1);
            }
        }
        
        result = max(result, increase + decrease - 1);
        return {increase, decrease};
    }
};

Summary

  这道题目是二叉树中有关路径长度的题目，一般来说这类题目都是能使用递归求解，而递归函数的返回值会包含多个信息，在这里就是包含了递增和递减的路径长度。这道题目的分享到这里，感谢你的支持！

Welcome to my other publishing channels