LeetCode解题报告（472）-- 1612. Check If Two Expression Trees are Equivalent

Problem

A binary expression tree is a kind of binary tree used to represent arithmetic expressions. Each node of a binary expression tree has either zero or two children. Leaf nodes (nodes with 0 children) correspond to operands (variables), and internal nodes (nodes with two children) correspond to the operators. In this problem, we only consider the '+' operator (i.e. addition).

You are given the roots of two binary expression trees, root1 and root2. Return true if the two binary expression trees are equivalent. Otherwise, return false.

Two binary expression trees are equivalent if they evaluate to the same value regardless of what the variables are set to.

Example 1:

1 2	Input: root1 = [x], root2 = [x] Output: true

Example 2:

1
2
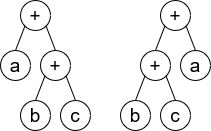
3

Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,c]
Output: true
Explaination: a + (b + c) == (b + c) + a

Example 3:

1
2
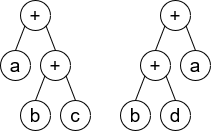
3

Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,d]
Output: false
Explaination: a + (b + c) != (b + d) + a

Constraints:

The number of nodes in both trees are equal, odd and, in the range [1, 4999].
Node.val is '+' or a lower-case English letter.
It’s guaranteed that the tree given is a valid binary expression tree.

Follow up: What will you change in your solution if the tree also supports the '-' operator (i.e. subtraction)?

Analysis

题目给出两颗算术表达式的树，里面只有+这个运算，要求我们比较两棵树的计算结果是否一样。只有+这个运算符限制让这道题目变得很简单，因为+的结合律是不讲究顺序的，所以我们可以只统计变量出现的次数去判断运算结果是否一样。对第一颗树遍历，然后把变量的出现次数统计一遍，再遍历第二颗树，对每个变量的出现自减，如果最后出现次数是0，说明正好抵消了，如果有变量的出现次数大于0，说明无法抵消，return false。

然后题目还给了一个follow up让我们来处理包含-运算的情况。加上了-就不一样了，因为减法后面有括号的话，括号里的运算符都要变号。所以，如果是左子树就没有这个问题，如果当前的符号是-，其右子树的符号就要改变，所以在统计的时候我们只需要考虑上符号就可以了，加号就是频率+1，减号就是频率-1，还是统计变量的出现次数。

Solution

无。

Code

/**
 * Definition for a binary tree node.
 * struct Node {
 *     char val;
 *     Node *left;
 *     Node *right;
 *     Node() : val(' '), left(nullptr), right(nullptr) {}
 *     Node(char x) : val(x), left(nullptr), right(nullptr) {}
 *     Node(char x, Node *left, Node *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool checkEquivalence(Node* root1, Node* root2) {
        helper(root1, 1);
        helper(root2, -1);
        
        for (auto &[k, v]: m) {
            if (v != 0) {
                return false;
            }
        }
        return true;
    }
private:
    unordered_map<int, int> m;
    void helper(Node* root, int add) {
        if (!root) {
            return;
        }
        
        if (root->val >= 'a' && root->val <= 'z') {
            m[root->val] += add;
        }
        helper(root->left, add);
        helper(root->right, add);
    }
};

Summary

这道题目包括follow up的基本思路是统计变量的出现次数，当处理follow up时还要考虑到-对右子树的影响。这道题目的分享到这里，感谢你的支持！