LeetCode解题报告（475）-- 1901. Find a Peak Element II

Problem

A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.

Given a 0-indexed m x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array [i,j].

You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.

You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.

Example 1:

1
2
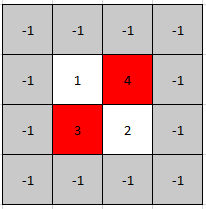
3

Input: mat = [[1,4],[3,2]]
Output: [0,1]
Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.

Example 2:

1
2
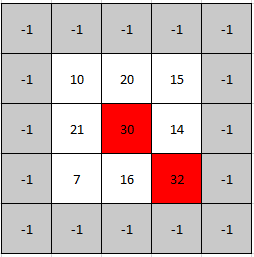
3

Input: mat = [[10,20,15],[21,30,14],[7,16,32]]
Output: [1,1]
Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 500
1 <= mat[i][j] <= 105
No two adjacent cells are equal.

Analysis

题目给出一个矩阵，要求找到矩阵里面的peak element，定义peak element是它比它四周的值都要大的位置。最直接的做法就是遍历一遍，每个位置都检查下，但这个复杂度就是$O(MN)$了。题目要求了复杂度是$O(mlog(n))$或者是$O(nlog(m))$。看到log复杂度应该要往二分查找靠，并且这个还是找最大值，所以可以很确定是用二分查找了。

这里我对列做二分查找，对第mid列，遍历每一行，找到最大的行maxRow，这个[maxRow][mid]就是一个候选，我们再看它和左右的元素作比较（不需要和上下作比较，因为找到最大的行已经完成了这个部分），如果左边的值比较大，right = mid - 1往左寻找，如果右边的值比较大，left = mid + 1往右寻找，最后如果都不到就返回[-1, -1]。

Solution

无。

Code

class Solution {
public:
    vector<int> findPeakGrid(vector<vector<int>>& mat) {
        int left = 0, right = mat[0].size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            int maxRow = 0;
            for (int i = 0; i < mat.size(); ++i) {
                if (mat[i][mid] > mat[maxRow][mid]) {
                    maxRow = i;
                }
            }
            
            bool toLeft = mid - 1 >= left && mat[maxRow][mid - 1] > mat[maxRow][mid];
            bool toRight = mid + 1 <= right && mat[maxRow][mid + 1] > mat[maxRow][mid];
            
            if (!toLeft && !toRight) {
                return {maxRow, mid};
            } else if (toLeft) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return {-1, -1};
    }
};

Summary

这道题目的二分很简单，当然也可以对行做二分，每次找到最大的列，其本质是一样的。这道题目的分享到这里，感谢你的支持！