LeetCode解题报告（495）-- 490. The Maze

Problem

There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right, but it won’t stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the m x n maze, the ball’s start position and the destination, where start = [startrow, startcol] and destination = [destinationrow, destinationcol], return true if the ball can stop at the destination, otherwise return false.

You may assume that the borders of the maze are all walls (see examples).

Example 1:

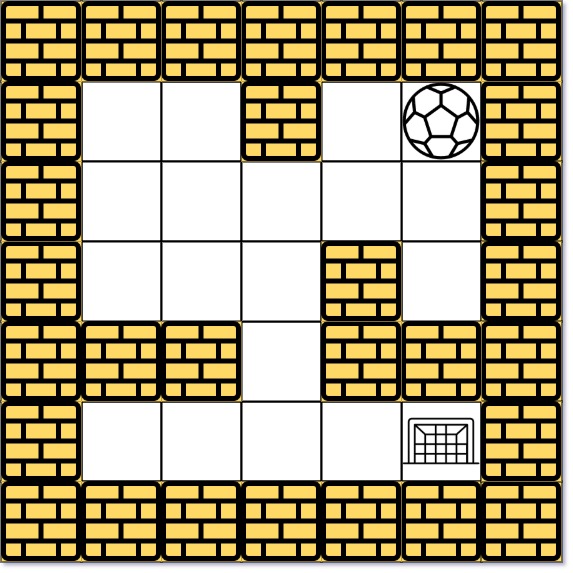
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.

Example 2:

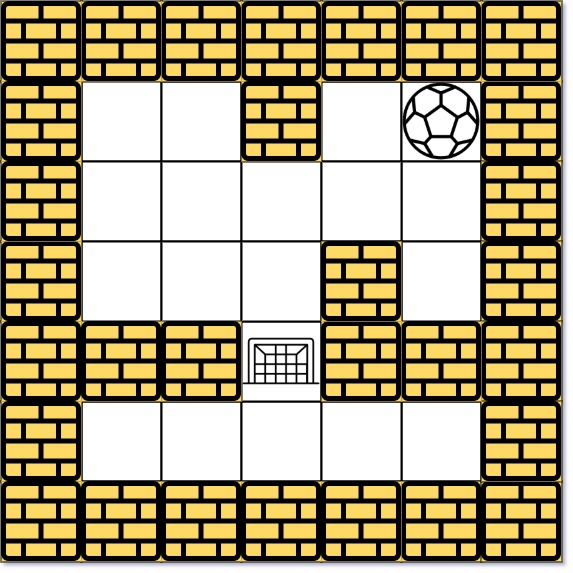
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2]
Output: false
Explanation: There is no way for the ball to stop at the destination. Notice that you can pass through the destination but you cannot stop there.

Example 3:

Input: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1]
Output: false

Constraints:

• m == maze.length
• n == maze[i].length
• 1 <= m, n <= 100
• maze[i][j] is 0 or 1.
• start.length == 2
• destination.length == 2
• 0 <= startrow, destinationrow <= m
• 0 <= startcol, destinationcol <= n
• Both the ball and the destination exist in an empty space, and they will not be in the same position initially.
• The maze contains at least 2 empty spaces.

---

Analysis

  这道题目给出一个迷宫，足球作为起点，球门作为终点，每次球可以向周围四个方向移动一格，问球最终能否到达球门的位置。这其实就是一道非常经典的二维矩阵BFS问题，每次把当前位置的邻居都放入到队列中，放入前判断合法性，最终如果能找到则返回true，如果一直都找不到直到队列为空，则返回false。

Solution

  无。

---

Code

class Solution {
public:
    bool hasPath(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {
        int m = maze.size(), n = maze[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        int dx[] = {-1, 0, 1, 0};
        int dy[] = {0, -1, 0, 1};
        
        queue<pair<int, int>> q;
        q.push({start[0], start[1]});
        
        while (!q.empty()) {
            auto cur = q.front();
            q.pop();
            int x = cur.first, y = cur.second;
            if (x == destination[0] && y == destination[1]) {
                return true;
            }
            
            for (int k = 0; k < 4; k++) {
                int newX = x + dx[k];
                int newY = y + dy[k];
                
                while (newX >= 0 && newX < m && newY >= 0 && newY < n && maze[newX][newY] == 0) {
                    newX += dx[k];
                    newY += dy[k];
                }
                
                if (!visited[newX - dx[k]][newY - dy[k]]) {
                    q.push({newX - dx[k], newY - dy[k]});
                    visited[newX - dx[k]][newY - dy[k]] = true;
                }
            }
        }
        
        return false;
    }
};

---

Summary

  这道题目是经典的常规BFS，是一道学习BFS遍历框架很好的题目。这道题目的分享到这里，感谢你的支持！