Halo

A magic place for coding

0%

LeetCode解题报告（496）-- 505. The Maze II

Posted on Edited on Valine:

Problem

There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right, but it won’t stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the m x n maze, the ball’s start position and the destination, where start = [startrow, startcol] and destination = [destinationrow, destinationcol], return the shortest distance for the ball to stop at the destination. If the ball cannot stop at destination, return -1.

The distance is the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included).

You may assume that the borders of the maze are all walls (see examples).

Example 1:

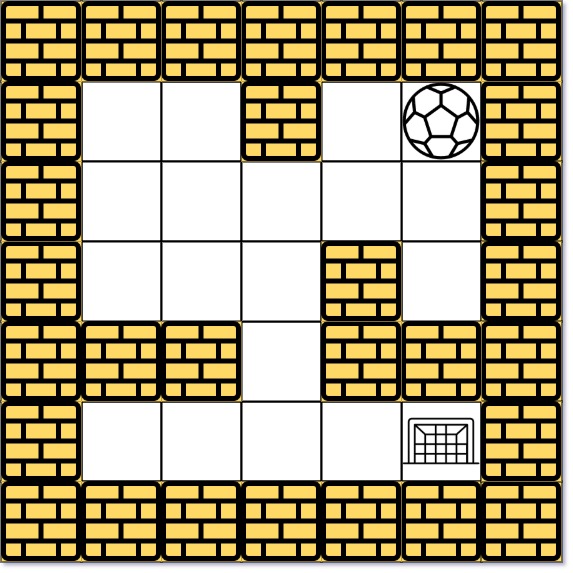
Example1

1
2
3
4
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
Output: 12
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
The length of the path is 1 + 1 + 3 + 1 + 2 + 2 + 2 = 12.

Example 2:

Example2

1
2
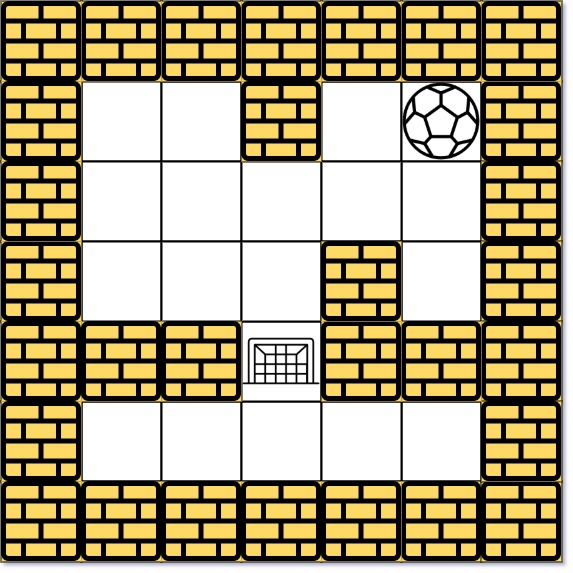
3
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2]
Output: -1
Explanation: There is no way for the ball to stop at the destination. Notice that you can pass through the destination but you cannot stop there.

Example 3:

1
2
Input: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1]
Output: -1

Constraints:

  • m == maze.length
  • n == maze[i].length
  • 1 <= m, n <= 100
  • maze[i][j] is 0 or 1.
  • start.length == 2
  • destination.length == 2
  • 0 <= startrow, destinationrow <= m
  • 0 <= startcol, destinationcol <= n
  • Both the ball and the destination exist in an empty space, and they will not be in the same position initially.
  • The maze contains at least 2 empty spaces.

Analysis

  这道题目是迷宫系列题的第二题，第一题非常简单就是一个BFS，那这道题目又有什么不同呢？区别在于这道题目球的移动不是一格一格，而是往一个方向一直移动到障碍。所以我们在BFS的时候，不能只是检查当前位置的四个邻居，而是往四个方向一直延伸，直到碰到障碍，再把那个位置加入到队列中（也要判断合法性）。

  同时，因为这里返回的不是能否到达，而是最短距离，所以我们还要用一个记忆数组记录每个位置距离起点的最短距离，最后返回。这个记忆数组还有另一个作用，虽然BFS天然地保证了最短路径的遍历，但在这道题目的条件下并不成立，因为这里的BFS并不是一格一格走的，所以我们要把路径长度记录到这个记忆数组中，只有比当前记忆数组记录的值小，我们才选择把侯选位置加入到队列中。

Solution

  无。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    int shortestDistance(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {
        int m = maze.size(), n = maze[0].size();
        vector<vector<int>> visited(m, vector<int>(n, INT_MAX));
        int dx[] = {-1, 0, 1, 0};
        int dy[] = {0, -1, 0, 1};
        
        queue<vector<int>> q;
        q.push({start[0], start[1], 0});
        visited[start[0]][start[1]] = 0;
        while (!q.empty()) {
            auto cur = q.front();
            q.pop();
            int x = cur[0], y = cur[1], dis = cur[2];
            
            for (int k = 0; k < 4; k++) {
                int newX = x + dx[k];
                int newY = y + dy[k];
                
                int temp = dis;
                while (newX >= 0 && newX < m && newY >= 0 && newY < n && maze[newX][newY] == 0) {
                    newX += dx[k];
                    newY += dy[k];
                    temp++;
                }
                // --temp;
                
                if (temp < visited[newX - dx[k]][newY - dy[k]]) {
                    q.push({newX - dx[k], newY - dy[k], temp});
                    visited[newX - dx[k]][newY - dy[k]] = temp;
                }
            }
        }
        
        return visited[destination[0]][destination[1]] == INT_MAX ? -1: visited[destination[0]][destination[1]];
    }
};

Summary

  这道题目是在BFS上面的一个小创新，创新的点在于下一个位置并不是四个邻居，而是四个方向一直延伸。这道题目的分享到这里，感谢你的支持！

Welcome to my other publishing channels