Halo

A magic place for coding

0%

找出出现次数超过一半的数字

Posted on Edited on Valine:

题目

  数组经典题目：数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。如一个长度为9的数组{1, 2, 3, 2, 2, 2, 5, 4, 2}。由于数字2在数组中出现了5次，超过了数组长度的一半，输出为2。

输入：

 每个case包含两行：

 第一行输入一个整数n($1\le n\le100000$)，表示数组中元素的个数。

 第二行输入n个整数，表示数组中的每个元素，这n个整数的范围是有符号整数的范围。

思路

  第一种思路是用排序的方法。因为该数字出现的次数超过了一半，那么排序后他必定是位于数组的中间。排序的复杂度是$O(nlogn)$。

  第二种思路，用统计的方法。我们可以使用一个map来遍历这个数组，统计完每个数字出现的次数，再找出数量最多的那个。复杂度为$O(n)$。这里我们对第一种方法实现了时间复杂度的优化。

  第三种思路是一种擂台思路。假设每两个不同的数能够抵消，那么由于某个数字出现的次数超过了一半，那么最后擂台上剩下的那个数字必定就是我们要找的数字了。我们记录擂台上的情况，present表示当前擂台上的数字，count表示擂台上数字的个数（必然是相同的数字才能够同时存在擂台上）。然后我们遍历数组，如果前两个数抵消了，那么下一个数上擂台，最后遍历完后剩下的present就是答案。

  第三种方法的时间复杂度是$O(n)$，但是比起第二种方法，它不需要额外的空间。

代码

  前两个实现都很简单，这里就只放第三种实现的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <vector>
using namespace std;

int findTheNumber(vector<int> arr) {
  int size = arr.size();
  if (size == 0)
    return -1;
  int present = arr[0];
  int count = 1;

  for (int i = 1; i < size; i++) {
    if (present != arr[i]) {
      count--;
    }
    else {
      count++;
    }
    if (count == 0) {
      present = arr[i+1];
    }
  }
  return present;
}

int main() {
  int n = 0;
  cin >> n;
  vector<int> v;
  while (n--) {
    int tmp = 0;
    cin >> tmp;
    v.push_back(tmp);
  }
  cout << findTheNumber(v) << endl;
  return 0;
}

运行结果：

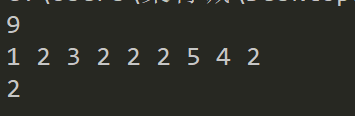
MoreThanHalf1

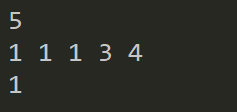
MoreThanHalf2

小结

  这道题求解并不难，但是仔细思考一下还是有更好的方法去求解的（优化空间复杂度和时间复杂度），所以就放在这里和大家分享了，谢谢您的支持！

Welcome to my other publishing channels