介绍
之前我介绍了使用二分法求解一个非线性方程,今天,我就来介绍另一种方法–牛顿法。
分析
牛顿法的核心思想是将非线性问题转化为线性问题处理。对于非线性方程$f(x)=0$,假设已知有近似根$x_k$(假定$f^{‘}(x_k) \ne 0$),将函数$f(x)$在点$x_k$进行泰勒展开,有
$$
f(x) \approx f(x_k) + f^{‘}(x_k)(x-x_k),
$$
于是方程$f(x) = 0$可以近似地表示为
$$
f(x_k) + f^{‘}(x_k)(x-x_k) = 0,
$$
上面这个是一个线性方程,记其根为$x_{k+1}$,则求得$x_{k+1}$的计算公式为:
$$
x_{k+1} = x_k - \frac{f(x_k)}{f^{‘}(x_k)},
$$
以上的迭代方法就称为牛顿法。
代码实现
Matlab代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
function [y, count, error, time] = Newton(x, e)
del_x = 0.0000001;
count = [];
time = [];
error = [];
k = 0;
err = 0;
y = x;
x = y + 1000;
n = 50;
tic
while 1
if (abs(y-x) <= e)
disp('满足迭代精度');
break;
elseif (k > n)
disp('迭代次数过多,迭代结束');
break;
else
x = y;
if((myFun(x+del_x) - myFun(x)) == 0)
disp('导数为0');
break;
else
y_deriv = (myFun(x+del_x) - myFun(x)) / del_x;
y = x - myFun(x) / y_deriv;
k = k + 1;
count(k) = k;
err = abs(y-x) / y;
error(k) = err;
end
end
end
toc
temp = toc / k;
for i=1:k
time(i) = i*temp;
end
disp('牛顿迭代结束');
end
function [y] = myFun(x)
y = x*x - 115;
end
|
其中myFun是需要求解的非线性方程。
小结
求解上面代码中的非线性方程,即求$\sqrt115$的值,其算法分析结果如下:
迭代步数与误差的关系
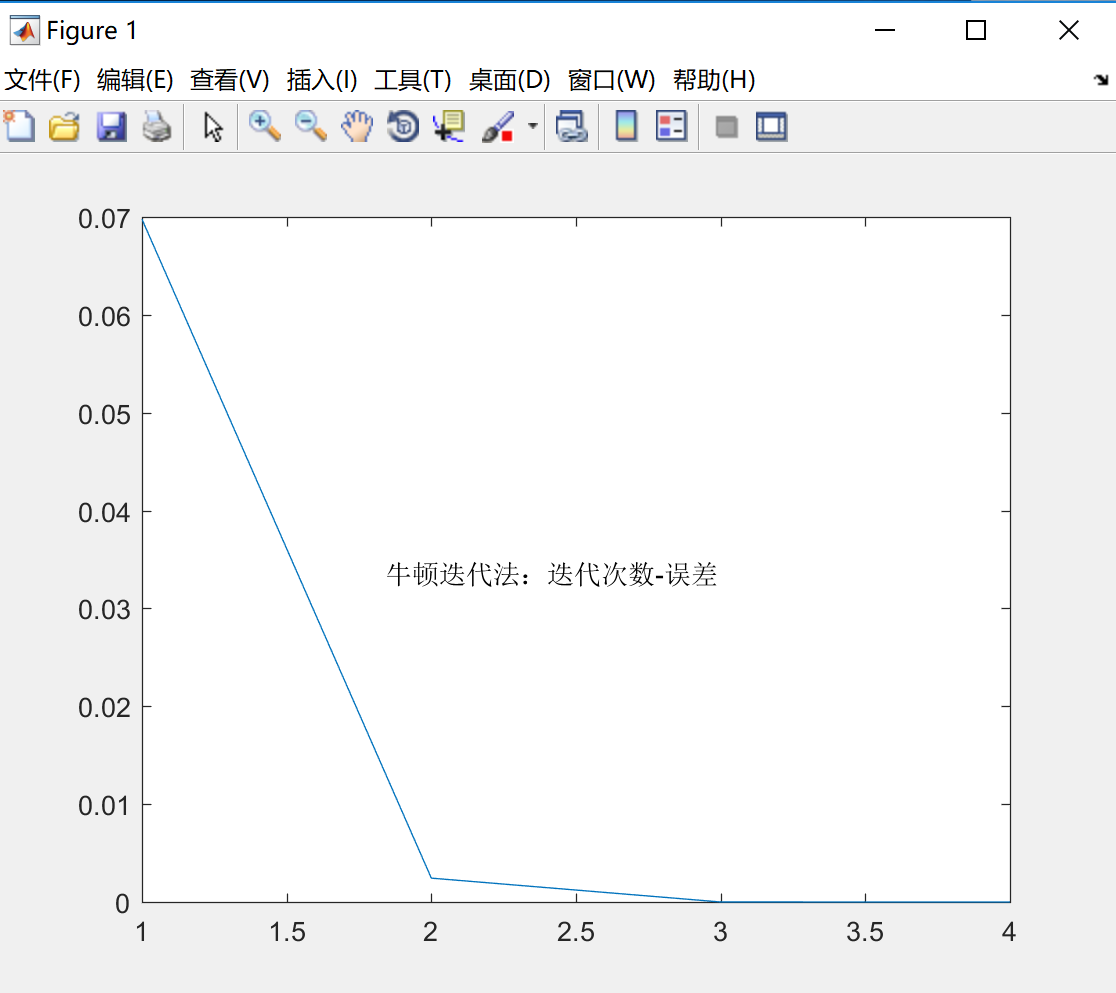
计算时间与误差的关系
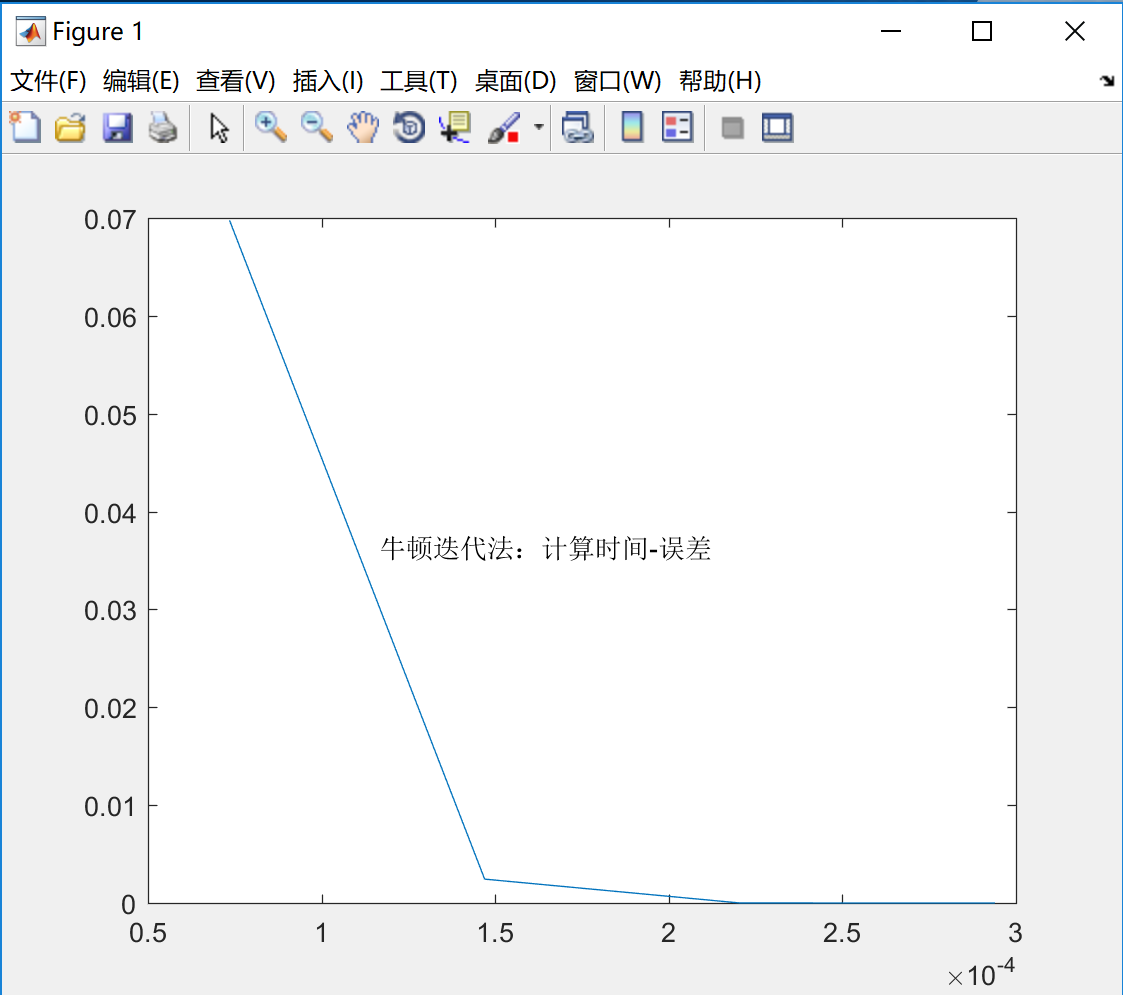
牛顿法的收敛速度要比二分法快很多,牛顿法在根$x^*$的邻近是平方收敛的,但在重根情况下,牛顿法只是线性收敛。
参考资料:
1.数值分析(第5版) 李庆扬,王能超,易大义 编



